Universidade Federal Rural do Rio de Janeiro
Programa de Pós-Graduação de Ciências Sociais em Desenvolvimento, Agricultura e Sociedade
Revista IDeAS, Rio de Janeiro, volume 15, 1-33, e021005, jan./dez. 2021 • ISSN 1984-9834
Artigo original • Revisão por pares • Acesso aberto
Pobreza hídrica en 78 municipios del Noroeste de México: una reflexión a partir del Índice de Pobreza Hídrica y la Pobreza Multidimensional, 2015
Water poverty in 78 municipalities in Northwest Mexico: a reflection from the Water Poverty Index and Multidimensional Poverty, 2015
María Juliana Olivas-Palma[1], Mario Camberos-Castro[2]
Resumen El objetivo de este trabajo es estimar el grado de pobreza hídrica en los 78 municipios de la Región Hidrológico-Administrativa 2, Noroeste de México, año 2015, e identificar los vínculos entre los Índices de Pobreza hídrica (IPh) y Pobreza multidimensional (IPm). Metodología: se implementa el IPh de Lawrence, Meigh y Sullivan (2003). Resultados: el IPh presentó valores entre 0.36 y 0.71; 39 municipios presentaron un IPh muy bajo y bajo, lo que equivale al 25% de la población total, del cual 16% es rural y 6% está en pobreza extrema. Los índices comparten las variables ingreso, salud, escolaridad, agua y saneamiento y 44.5% de la variación del IPh se explica por el IPm. Conclusiones: a medida que mejora el IPm en las variables comunes al IPh, en esa misma proporción se beneficia éste. Por lo tanto, estos son los componentes del IPh sobre los cuales se necesitan focalizar las políticas públicas para mejorar la pobreza hídrica. Palabras clave: Nexos agua-pobreza; Rezago social; Enfoque de capacidades; Escasez de agua; Seguridad hídrica. Abstract The objective of this work is to estimate the degree of water poverty in the 78 municipalities of the Hydrological-Administrative Region 2 Northwest of Mexico, year 2015, and to identify the links between the Indices of Water Poverty and Multidimensional Poverty (IPh, IPm). Methodology: implementation of the IPh of Lawrence, Meigh and Sullivan(2003). Results: the IPh presented values between 0.36 and 0.71; 39 municipalities presented very low and low IPh and represent 25% of the total population, of which 16% is rural and 6% is in extreme poverty. The indices share the variables income, health, education, water and sanitation and 44.5% of the variation of the IPh is explained by the IPm. Conclusions: as the IPm improves in the variables in common with the IPh, the latter benefits in the same proportion. Therefore, these are the IPh components upon which public policies need to focus, to improve water poverty. Keywords: Water-poverty links; Social backwardness; Capability Approach; Water scarcity; Water security. | Submissão: Aceite: Publicação: |
Citação sugerida OLIVAS-PALMA, María Juliana; CAMBEROS-CASTRO, Mario. Pobreza hídrica en 78 municipios del Noroeste de México: una reflexión a partir del Índice de Pobreza Hídrica y la Pobreza Multidimensional, 2015. Revista IDeAS, Rio de Janeiro, v. 15, p. 1-33, e021005, jan./dez. 2021. Licença: Creative Commons - Atribuição/Attribution 4.0 International (CC BY 4.0). |
Introducción[3]
Algunas regiones, sin importar su clasificación con respecto al desarrollo, carecen de disponibilidad de volúmenes de agua renovable per cápita suficientes para satisfacer las necesidades básicas, como lo muestran las estadísticas del agua de Aquastat (FAO 2016). En un claro contraste, en otras regiones, aún con abundantes recursos renovables, el agua se ha convertido en un problema, como ocurre en algunas de las Regiones Hidrológico Administrativas (RHA) de México (CONAGUA 2016, p. 20).
Si bien debe reconocerse que no existe un consenso general sobre cuál es este problema, ni la magnitud del mismo, en lo que sí concuerdan la mayoría de los involucrados e interesados es que no solo depende de la disponibilidad y cobertura de agua, sino también de los componentes socioeconómicos de acceso a la vivienda, el ingreso, la educación y cultura del agua y la salud, el deterioro ambiental y el uso que se le da al agua (MARVIN, 1994; LISTER, 1995; SULLIVAN 2001; SULLIVAN; MEIGH, 2003; MOLLE; MOLLINGA, 2003; LAWRENCE; MEIGH; SULLIVAN, 2003; MOLLE; MOLLINGA; MEINZEN-DICK, 2008)
En consecuencia, el problema se refiere a la población que carece de agua segura en sus hogares y para consumo humano en general, o en los espacios públicos, o agua limpia en las áreas verdes, ríos, lagos y lagunas; es decir, a la escasez de agua apta para consumo humano y mantenimiento de los ecosistemas.
Es importante señalar que la pobreza hídrica es un problema que va más allá de la carencia del agua como recurso natural, que trasciende lo económico y social y, por lo tanto, requiere ser evaluada sintetizando información de diferentes componentes, dimensiones e indicadores. Para lograrlo, es deseable la elaboración de un índice que proporcione una idea de qué tan satisfecha está la población con la disponibilidad de agua o, caso contrario, qué le falta a la población para conseguirlo y cuáles son los componentes del índice sobre los que se debe actuar por medio de una política pública para lograr una mejor satisfacción.
Los objetivos de este artículo son dos. El primero, estimar el grado de Pobreza hídrica en los 78 municipios de la Región Hidrológico Administrativa 2, Noroeste (RHA2N) de México, para el año 2015; el segundo, identificar la relación formal entre los Índices de Pobreza multidimensional (Pm) y de Pobreza hídrica (Ph). Con ellos se pretende dar respuesta a preguntas como las siguientes: ¿Cuáles son los municipios que presentan mayor pobreza hídrica en la RHA2N? ¿Cuál es la relación formal entre el IPm y el IPh? ¿Cuáles son las dimensiones de la Ph que deben ser atendidas prioritariamente mediante una política pública a la escala del estudio?
La hipótesis de trabajo argumenta que los municipios con mayor pobreza multidimensional presentarán una alta pobreza hídrica, independientemente de la cantidad de recursos hídricos de que dispongan en forma natural. Ello en virtud de que la Ph está relacionada con los aspectos socioeconómicos los cuáles, de ser atendidos, permitirán que el agua llegue a las localidades y en consecuencia a la población para los diversos usos.
Con la intención de que los tomadores de decisiones cuenten con información objetiva que les permita implementar políticas públicas focalizadas en la región del estudio, y que coadyuven a la disminución de la Ph, se considera relevante abordar su prevalencia desde la perspectiva de la Pm y a la escala municipal. Debe considerarse que por disposiciones legales y normativas son los municipios quienes tienen a su cargo las funciones y servicios públicos de agua potable, drenaje, alcantarillado, tratamiento y disposición de aguas residuales, entre otros, según lo dispuesto en el artículo 115 de la Constitución Política de los Estados Unidos Mexicanos.
El artículo se desarrolla en las siguientes etapas. Después de la introducción, en primer lugar, se presenta un recuento de características hidrológicas de la región en estudio, para enseguida revisar la discusión sobre el concepto de Pobreza Hídrica a nivel internacional y luego proporcionar un breve recuento de los estudios de pobreza hídrica en México.
Posteriormente se desarrolla la metodología para estimar el IPh, que incluye el procedimiento de selección de dimensiones e indicadores, recopilación de información, tratamiento estadístico de homogenización y normalización de valores extremos, junto con las ecuaciones para estimar el IPh. Se finaliza esta sección metodológica con un apartado en el que se muestra la relación formal entre los índices de pobreza multidimensional y pobreza hídrica. Seguidamente se elaboran los cálculos y se presenta un apartado con los resultados de las estimaciones de los IPh para los 78 municipios que conforman la RHA2N, así como un análisis y discusión de los mismos. Finalmente, se presentan las conclusiones.
1.1 Características de la Región Hidrológico-Administrativa 2, Noroeste de México.
La Región Hidrológico-Administrativa 2 Noroeste (RHA2N) seleccionada para medir la pobreza hídrica, se ubica en la porción Noroeste de la República mexicana. Comprende los estados de Sonora y parte de Chihuahua; 86% de su superficie pertenece a Sonora y 14% a Chihuahua. Es la segunda RHA más extensa del país después de la RHA VI Río Bravo. Administrativamente, está conformada por 78 municipios: 71 corresponden al estado de Sonora (de un conjunto estatal de 72) y 7 al estado de Chihuahua (de un total estatal de 67).
La RHA2N integra 21 cuencas hidrológicas, abarcando una superficie de 175,955 km2. Las principales corrientes de agua son los arroyos Cocoraque, Cocóspera, Quiriego y los ríos Bavispe, Concepción, Magdalena, Mátape, Mayo, San Miguel, Sonora, Sonoyta y Yaqui. La Región se caracteriza por su clima de tipo seco y semiseco en la mayor extensión de su superficie, y subhúmedo y templado a lo largo del límite oriental, en la alta sierra. La RHA2N tiene una temperatura extremosa, aunque su media anual es de 20°C. La precipitación media anual es baja, de 368 mm aproximadamente y además distribuida geográficamente de manera desigual, presentándose al Noroeste de la región las menores precipitaciones (100 mm por año), en las cuencas conocidas como el Río Sonoyta y del Desierto de Altar, así como el Río Concepción, y aumentando a más de 1,000 mm anuales hacia el Sur-Sureste, en la cuenca del Río Mayo. Cabe resaltar que en la zona serrana en los estados limítrofes de Sonora y Chihuahua, la precipitación se manifiesta en forma de lluvia y de nieve.
Socioeconómicamente, parte de la RHA2N la ocupa el estado de Sonora, ubicado en lo que se conoce como región noroeste de México, por lo que centraremos nuestro interés en el mismo. La información utilizada es del año 2015, último año en que se registra información a nivel municipal para los municipios de México. Sonora registraba una población total en 2015 de 2,850,330, distribuida en 72 municipios; el 93% de la población habita en 18 municipios urbanos con 15,000 habitantes o más, y el 7% restante en 54 municipios rurales con menos de 15,000 habitantes cada uno (INEGI, 2015). En el Cuadro 2 se presentan los municipios que conforman la región en estudio. Desde el punto de vista económico, la entidad registró en el 2017, último año comparable a precios constantes de 2013, un producto interno bruto (PIB) per cápita de 193,294 pesos, ubicado por encima del promedio nacional de 146,378 pesos y sólo superado por la ciudad de México, Nuevo León, Coahuila, Baja California Sur y Campeche. En esta última entidad, el alto PIB es atribuible al petróleo y se debe de mencionar, porque gran parte del mismo termina en la Hacienda federal, lo que significa que se distribuye a nivel nacional y no solo en Campeche.
1.2 El concepto de Pobreza Hídrica
Una revisión del concepto de pobreza pone de manifiesto diversas acepciones en el transcurso del tiempo. Sin embargo, pese a la posible controversia en su definición, existe coincidencia en relacionarla con una condición de carencia o escasez evaluadas objetivamente (TOWNSEND, 1979, p. 31). Bajo esta premisa, dependiendo del tipo de carencia, se ha conceptualizado la pobreza como carencia o falta de ingresos, a partir de la cual se generaliza el concepto de pobreza y se crea un índice para su medición (SEN, 1976). Posteriormente, Sen (1993) la conceptualiza a partir del enfoque de capacidades, todas ellas basadas en la teoría del bienestar de Pigou (1929). La más conocida actualmente, la pobreza multidimensional (ALKIRE; FOSTER, 2008), es establecida en México desde 2008 como metodología para medir la pobreza (CONEVAL, 2009). Esta metodología contiene varias dimensiones contempladas en el concepto de pobreza hídrica, razón por la cual podemos establecer un nexo entre los índices de pobreza multidimensional (IPm) y el de pobreza hídrica (IPh).
La definición más aceptada de pobreza hídrica o pobreza del agua es “la situación en la que una nación o región no puede pagar el costo de proporcionar agua potable de manera sostenible para todas las personas en todo momento” (FEITELSON; CHENOWETH, 2002, p. 263). Suponiendo que la escasez del agua es un problema a nivel global, Rijsberman (2006) escribe acerca de la dificultad de determinar si el agua es realmente escasa en el sentido físico a escala mundial, o si se trata de un problema de suministro, o si bien, estando disponible, se trata de un problema de atención a la demanda. Por otro lado, puntualiza el autor, “que la extracción de agua para uso doméstico, alimentario e industrial tiene un gran impacto en los ecosistemas en muchas partes del mundo, inclusive, en aquellos países que no se consideran con escasez de agua” (RIJSBERMAN, 2006, p. 5).
Para entender mejor el concepto de Ph, ésta ha sido caracterizada bajo los siguientes criterios: 1. El agua se puede suministrar en cantidades crecientes a un costo cada vez mayor; 2. La mala calidad del agua restringe el uso del agua si se quiere conservar la salud y el bienestar; 3. El uso del agua no puede limitarse a la perspectiva de las generaciones actuales; 4. En muchos países con abundantes precipitaciones pluviales, gran parte de la población no tiene acceso al agua, ni siquiera para satisfacer las necesidades básicas de salud y saneamiento; y 5. El agua se puede utilizar más de una vez, pero esto requiere que los efluentes sean tratados (FEITELSON; CHENOWETH, 2002, p. 268).
En investigaciones posteriores, referidas específicamente a la pobreza hídrica, Molle y Mollinga (2003) clasifican los usos fundamentales del agua en U1-potable, U2-doméstica, U3-producción, U4-económica y U5-necesidades ambientales y los combinan en una matriz con los tipos de escasez (S1-física, S2-económica, S3-gestión institucional, y S4-política). Por ejemplo, una de estas combinaciones sería U1S2, cuya lectura es: el agua potable para consumo humano está disponible pero una persona no puede pagarla. Los autores concluyen que el nexo agua-sociedad no puede ni debe reducirse solamente a los medios técnicos y financieros para suministrar cualquier cantidad de agua que se solicite.
Lo anterior está en una clara concordancia con lo expresado por Lissner et al. (2014) quienes afirman que para tomar decisiones informadas con respecto al agua, se requieren enfoques integrados que permitan ver los determinantes en su conjunto. Por lo tanto, ofrecen su visión desde dos perspectivas: un enfoque para medir las condiciones de vida humana, adecuadas para el bienestar y el desarrollo y un segundo enfoque que incluye aspectos de cantidad, calidad y acceso al agua de manera integrada.
En ese sentido, Marvin (1994) hace énfasis en la amenaza que el problema de la Ph representa para la población, especialmente para los enfermos, y recalca el hecho de que no se puede suponer que por existir redes de infraestructura urbana se debe dar por sentado el acceso equitativo a los servicios públicos; lo cual queda bastante claro, ya que estos servicios, incluido el suministro de agua, están comúnmente insertos en la dinámica del mercado, en la cual a veces solo es posible obtenerlos si se tienen ingresos.
En el mismo contexto, la literatura en el tema muestra que simultáneamente se ha creado una nueva conceptualización, medición y evaluación de la Ph, por lo que conocer sólo el dato de cuánta agua renovable está disponible para un determinado número de personas no proporciona una visión completa de la realidad de todos los indicadores y variables inherentes al agua (LAWRENCE; MEIGH; SULLIVAN, 2003). Como analogía se menciona el Producto Interno Bruto (PIB) per cápita, “que aún se usa en muchas circunstancias para evaluar la calidad de vida” (SEN, 1993), y que no proporciona detalle de la distribución de la renta, ni en manos de quién está el ingreso, como ocurre a menudo con el agua: se sabe cuánta hay, pero no quién la tiene acaparada ni en qué condiciones se encuentra.
Por otro lado, después de reconocer las limitaciones de indicadores referentes a la medición de la situación del agua, Mlote, Sullivan y Meigh (2002) desarrollan un índice para medir el grado de Ph, al que denominan ‘Water Poverty Index’ (Índice de Pobreza Hídrica, IPh), el cual definen como una herramienta de medición para evaluar la pobreza en relación con el agua, cuantificándola de menor disponibilidad a mayor disponibilidad, en el cual se establecen como dimensiones de la Ph las siguientes: 1) Los recursos hídricos del país o región; 2) el acceso al agua para consumo humano y saneamiento; 3) la capacidad económica y social de las personas para procurarse el agua; 4) el uso que se le da al agua; y 5) el medio ambiente y su nivel de conservación.
En el marco de las revisiones al IPh por otros investigadores, se han recomendado mejoras en el sentido de la selección de las variables para las dimensiones y en la asignación de las ponderaciones o pesos, propuestas que han coincidido en la aplicación del análisis de componentes principales. Entre ellos se encuentran los trabajos de Cho, Ogwang y Opio(2010); Pérez-Foguet; Giné-Garriga (2011); Jemmali; Matoussi (2013), entre otros.
Llama la atención que la definición de Feitelson y Chenoweth (2002), considerada una de las más importantes, pone énfasis en los aspectos económico y social, como también lo hacen la mayoría de los autores que analizamos. En este sentido, es pertinente mencionar que la Ph se puede manifestar aun teniendo disponibilidad de agua, si se carece de la infraestructura, o aun teniéndola, si una proporción o parte de la población no cuenta con los medios para pagarla, lo cual nos permite confirmar que la búsqueda de la relación entre el IPh y el de Pm es conducente dado que ambos índices son comparables, además de estar acotados 0 < (IPh, Pm) < 1.
1.3 Estudios de pobreza hídrica en México
Los estudios en este tema referidos a México, o que se hubiesen elaborado en nuestro país, no son muy abundantes, más bien son escasos. Por ejemplo, la investigación de Lawrence, Meigh y Sullivan (2003) clasifica a 140 países, teniendo en cuenta tanto factores físicos como socioeconómicos, asociados con la escasez de agua. En ella estimó el IPh para México en 57.5, el más bajo de los países de la OCDE, pero en mejores condiciones que la mayoría de los países de América Latina y el Caribe.
En México, Álvarez et al. (2013) hacen el cálculo de un índice de pobreza hídrica para el Valle de San Luis Potosí, una región semiárida donde el acuífero tiene una gran importancia económica. En ese trabajo se hace énfasis en la dimensión Medio Ambiente, en el indicador de calidad del agua, para representar los efectos de la contaminación y de la pérdida de vegetación en la región. Se encontró un índice de 46 puntos, menor al 57.5 de México anteriormente señalado.
Por su parte, Herrera, Córdova y Quevedo (2007) estimaron el Índice de Vulnerabilidad Climática para el Municipio de Cd. Juárez, Chihuahua, a partir del IPh ampliado en una dimensión más. Se calcularon los dos índices con datos oficiales estatales y nacionales, excepto el dato de la sensibilidad a inundaciones, para el cual se realizó una encuesta estructurada y focalizada en un grupo de expertos en el tema. Se encontró que la zona está en situación de riesgo y que demanda atención en la elaboración de planes que protejan el recurso hídrico contra los desastres naturales.
Dados estos antecedentes, la presente investigación contribuirá al conocimiento del problema del agua en México, pero a nivel local, en una de las regiones más áridas, la RHA2N.
2 Metodología y datos utilizados en el estudio
Como se mencionó en la introducción, en este trabajo se implementa el Índice de Pobreza hídrica, el cual consta de 5 dimensiones, a saber: Recursos (R), Uso (U), Acceso (A), Capacidad (C), y Medio Ambiente (E). Cada uno de estos indicadores está integrado por diversas variables, las cuáles pueden diferir de una prueba a otra del IPh, dado que la inclusión, o no, de determinada variable dependerá en gran medida de la disponibilidad de los datos públicos en las regiones y países en donde se va a probar el índice. Esto es así, porque desde el desarrollo original, los autores contemplaron y recomendaron que los cálculos se efectuaran con datos públicos. Aunque para los autores esta es una de sus fortalezas, para algunos críticos del IPh, es una debilidad, al igual que lo es la ponderación arbitraria del peso de los indicadores, que en el desarrollo original se asigna el 20% a cada uno.
Enseguida se describe brevemente el significado de cada una de las dimensiones: a) Recursos (R) se define como la disponibilidad física del agua superficial y subterránea, tomando en cuenta su extracción y balance hídrico; b) Acceso al agua (A), se define como el nivel de acercamiento de la población al recurso hídrico en forma de agua segura para uso humano; c) Capacidad de aprovisionamiento del agua (C), se refiere a la eficacia de la población en proveerse del agua a la que tiene acceso; d) Uso (U), se define como las formas en las cuales el agua es usada para diferentes propósitos por la población; y e) Ambiente (E) este factor trata de capturar una serie de indicadores ambientales que reflejan la gestión del agua en sus interacciones ecológicas. En ese contexto, los valores de las dimensiones y variables que toma el IPh van de cero a 100 puntos porcentuales, en donde valores de cero o cercanos a cero representan mayor pobreza hídrica.
2.1 Las ecuaciones para estimar el IPh
A continuación se anotan y describen las ecuaciones para el cálculo del IPh. La ecuación 1 corresponde al cálculo general del IPh.
| (1) |
Donde: IPh, WPI, es el índice de pobreza de agua para una región en particular, resultado de la suma ponderada de los cinco componentes que se involucran en su cálculo.
En el IPh propuesto por Lawrence, Meigh y Sullivan (2003) los componentes se ponderan con respecto a su importancia relativa, usando funciones de peso Wi correspondientes a cada componente (Xi) de la estructura del WPI para la región. La ecuación desarrollada quedaría de la siguiente manera:
| (2) |
El valor del índice está acotado 0 < IPh < 1.
Enseguida se describen las fases y procesos llevados a cabo para la consecución de los objetivos planteados. En una primera fase se eligieron las escalas temporal y geográfica, selección de las dimensiones y variables y localización de las fuentes de datos. La muestra es a conveniencia, no probabilística y está conformada por los 78 municipios de la RHA2N. Las dimensiones y variables seleccionadas están basadas en la prueba de Lawrence, Meigh y Sullivan (2003); dicho lo anterior, se muestran en el Cuadro 1.
Cuadro 1 – Dimensiones y variables elegidas para el IPh de la RHA2N.
Dimensión | Variable | Descripción |
Recurso | R1 | Agua disponible renovable (2015) ponderado por superficie de municipio y por población, (hm³/año per capita), favorable la mayor cantidad |
R2 | Caudal procesado de aguas residuales lt/s, deseable el mayor caudal | |
R3 | Grado de presión sobre el recurso hídrico, es mejor el menor grado de presión | |
Acceso | A1 | Proporción de la población que cuenta con agua entubada dentro de la vivienda |
A2 | Proporción de la población con drenaje conectado a la red pública | |
Capacidad | C1 | Índice de educación 2015, 1 es el más deseable |
C2 | Índice de ingreso 2015, 1 es el más favorable | |
C3 | Índice de salud 2015, 1 es lo mejor | |
Uso | U1 | Uso por abastecimiento público, litros diarios per cápita |
U2 | Uso agrícola ponderado por ingreso (eficiencia) | |
U3 | Uso industria ponderado por ingreso (eficiencia) | |
U4 | Uso para industria eléctrica (excepto hidroeléctricas) ponderado por ingreso | |
Ambiente | E1 | Riesgo de inundación |
E2 | Cobertura forestal | |
E3 | Vulnerabilidad climática |
Fuente: elaboración propia, basada en Lawrence, Meigh y Sullivan (2003).
Enseguida se proporciona una descripción detallada de las variables, así como la fuente de datos de cada una de las dimensiones del IPh para esta prueba.
Dimensión Recursos (R). En esta prueba se agregan 3 variables: R1 es una medida de la disponibilidad total de recursos hídricos renovables en hm³/año, ponderados por la superficie del municipio. Se asume una distribución homogénea del agua total renovable disponible de la RHA en proporción a cada municipio. Los datos para esta variable se obtuvieron del informe Estadísticas del Agua en México (CONAGUA, 2016) y la superficie de los municipios se obtuvo de INEGI México en Cifras (INEGI, 2020). R1 está acotada en sus valores extremos a los percentiles 2.5 y 97.2, como parte de las prácticas recomendadas en la construcción de indicadores compuestos (NARDO et al. 2008, p. 84), con el fin de reducir la influencia de valores extremadamente altos o bajos. Enseguida, R1 se normaliza mediante el método Min – Max (NARDO et al. 2008, p. 85).
La variable R2 se refiere a la Tasa de tratamiento de aguas residuales municipales, cuyos datos se obtuvieron de los Anuarios Estadísticos y Geográficos de Sonora y Chihuahua, correspondiente al año 2015 (INEGI, 2017). Estas variables están acotadas en sus valores extremos a los percentiles 2.5 y 97.2 y normalizadas mediante el método Min – Max.
En ese mismo marco, la variable R3 representa el grado de presión sobre el recurso hídrico y es una proporción del volumen de agua de uso consuntivo total en relación con el agua disponible renovable. La fuente de datos para el año 2015 de esta variable se encuentra en los Anuarios Estadísticos y Geográficos de Sonora y Chihuahua (ibid.) y en Estadísticas del Agua (CONAGUA, 2016).
En esta misma secuencia se describen las variables de la dimensión Acceso (A); para la cual se incluyen, en esta prueba, las variables A1 y A2, que representan la proporción de la población con acceso a agua segura[4] y a saneamiento seguro (drenaje en la vivienda)[5], respectivamente. La fuente de datos para estas variables son los Anuarios Estadísticos y Geográficos de Sonora y Chihuahua (INEGI, 2017). Es pertinente aclarar que se seleccionaron para estas variables los datos de mayor alineación con el Objetivo 6 del Desarrollo Sostenible (ODS) de la agenda 2030, esto es, los más altos estándares de servicios de agua y saneamiento para la población (PNUD, 2019a).
Dimensión Capacidad (C). En la presente prueba, para esta dimensión se agregan las variables C1, C2 y C3 que representan el Índice de educación, el Índice de ingresos y el Índice de salud municipal, respectivamente. La fuente de datos para estas variables es el Informe de Desarrollo Humano Municipal 2010 – 2015, Transformando a México desde lo Local (PNUD, 2019b).
La dimensión Uso (U) está integrada por cuatro variables. U1 representa el abastecimiento público per cápita diario en litros, es una variable acotada en sus valores extremos a los percentiles 2.5 y 97.2 y normalizada mediante Min – Max. Por su parte, U2, U3 y U4 representan el Uso agrícola, industrial y para energía eléctrica, respectivamente, como una proporción del ingreso. La fuente de datos para los usos consuntivos agrícola, público, industria y energía eléctrica (excepto hidroeléctricas), en hm³ al año, con datos provenientes del Registro Público de Derechos de Agua (CONAGUA, 2020).
La dimensión Ambiente (E) se sintetiza por tres variables, E1 se refiere al riesgo de inundación del municipio. Al cuantificar las unidades cualitativas, esta variable toma valores de muy alto=0, alto=0.3, medio=0.6 y bajo=1. Los datos provienen de SEMARNAT (2020). Por otro lado, E2 representa la cobertura forestal presente en el territorio municipal, estimada en Global Forest Watch (WRI, 2020) y es una variable acotada en valores extremos a los percentiles 2.5 y 97.2 y normalizado mediante Min – Max. Finalmente, la variable E3 de esta dimensión se refiere a la Vulnerabilidad climática. Al cuantificar las unidades cualitativas, esta variable toma valores de muy alto=0, alto=0.3, medio=0.6 y bajo=1.
En lo concerniente a los instrumentos de recolección, tratamiento de los datos, estimación del IPh y análisis de resultados se utilizó el software Excel de Microsoft®. Destacando las funciones estadísticas para la normalización y homogeneización, las tablas dinámicas para la ordenación de los municipios de acuerdo al IPh resultante y el complemento Real Statistics Resource Pack[6] para los análisis de correlación entre los índices de Pm y Ph.
2.2 Relación entre los índices de Pobreza multidimensional e hídrica
El índice de pobreza multidimensional incluye en su elaboración los índices de rezago social que parte de las carencias mencionadas en la vivienda, dos de las cuales, agua entubada y drenaje, forman parte de la dimensión de Acceso (A) del IPh, mientras que el de salud, el de educación y el de ingreso, son parte de la dimensión de Capacidad (C) del IPh; así mismo, se consideran los índices de ingreso, salud y educación para construir el índice de desarrollo humano (IDH); finalmente, dado que todos ellos forman parte del índice de pobreza multidimensional (Pm), es razón por la cual podemos establecer una relación entre los tres índices: de pobreza multidimensional (Pm), de desarrollo humano (IDH) y de pobreza hídrica (IPh).
La relación se puede formalizar de la siguiente manera:
Pm = p(Y, E, S, V) (3)
IDH = f(Y, E, S) (4)
IPh = h(R, A, C, U, E) (5)
con p, f y h funciones, y definidas las variables como
Pm: Índice de pobreza multidimensional con Y ingreso, E educación, S salud, V vivienda (la cual contiene variables para drenaje y agua entubada);
IDH: Índice de desarrollo humano con Y ingreso, E educación, S salud;
IPh: Índice de pobreza hídrica con R recursos, A acceso (la cual contiene variables para drenaje y agua entubada), C capacidad (la cual contiene variables para ingreso, educación y salud), U uso y E ambiente.
Estas relaciones se pueden especificar como:
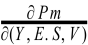 < 0 ;
< 0 ; 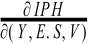 > 0 (6)
> 0 (6)
Siempre que aumenten Y, E, S y V, manteniéndose constantes las demás variables, el Pm disminuirá y el IPh aumentará; pero también se puede establecer la relación en un punto en el tiempo entre los dos índices:
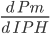 < 0 (7)
< 0 (7)
De lo anterior se desprende una conclusión más interesante, debido a que el Pm es asintóticamente decreciente (SEN, 1976; KAKWANI, 2008 apud CAMBEROS; BRACAMONTES, 2010) y cualquier incremento en alguno de los componentes, en varios de ellos o en todos, reducirá el Pm e incrementará el IPh, siempre que sus otros componentes se mantengan sin cambios. Dicho de manera más clara, todo cambio que reduzca la pobreza multidimensional mejorará la pobreza hídrica. Ambos índices están acotados 0 < (IPh, Pm) < 1.
La relación entre los índices la podemos probar por medio de un coeficiente de correlación de Pearson (r) entre los índices de Pm y los IPh de los 78 municipios que conforman la RHAN2, con resultados esperado signo negativo y valor -1 < r < 0.
3 Resultados
La elaboración del IPh se realiza a la escala geográfica municipal dentro de una región hidrológico administrativa, la RHA2N, compuesta por 71 municipios de Sonora y 7 de Chihuahua, aledaños a la llamada región sierra baja de Sonora, como se ve en la Figura 1. El municipio San Luis Río Colorado queda fuera, por estar adscrito a la RHA1, Baja California.
Otra aclaración pertinente es que para el municipio General Plutarco Elías Calles, en 2015 se carece de datos fuente respecto a la pobreza multidimensional de Coneval, por lo que se asume la aproximación de que sus valores permanecen iguales a los de 2010.
Por otra parte, realizaremos un análisis de características socioeconómicas más importantes de los municipios, que nos permitirá dimensionar los resultados del IPh.
El desarrollo social se mide por el menor índice de rezago social, o el porcentaje de carencia de la población que no consigue la dimensión o el indicador (CONEVAL, 2017a).
En primer lugar, se refiere a los índices de vivienda y sus servicios, de los cuales consideramos los 3 más importantes: agua entubada dentro de la vivienda, drenaje y electricidad. En esta dimensión de la vivienda, Sonora registraba en 2015 bajos índices de rezago social, con 3.1%, 6.6% y 1.3%, todos por debajo de la media nacional; pero ocultan la realidad de 4 municipios que registran rezagos que los ubica entre los 5 más atrasados de la entidad: Álamos, Quiriego, Rosario, Tesopaco y Yécora, que son aledaños a los 7 municipios de Chihuahua: Guerrero, Madera, Matachí, Moris, Ocampo, Temósachi y Uruachi, que forman parte de la RHA2N y que también muestran un rezago social importante.
El segundo índice, el grado de escolaridad, con 10 años en 2015, posiciona al estado arriba de la media nacional (9.1), de acuerdo a la Encuesta Intercensal 2015 (INEGI, 2015). Cabe aclarar algunas diferencias. Los municipios rurales registran 8.8 años y los urbanos 9.3, sin embargo, estos promedios ocultan municipios con rezago educativo en la entidad que no registran escolaridad, sino una tasa de analfabetismo elevada (mayor al promedio estatal de 2.2%); entre ellos destacan Rosario, con 9.2%, Quiriego, con 11.7% y Álamos, con 9.4%, mencionados con anterioridad.
Un tercer índice que consideramos es el de pobreza multidimensional (Pm). Para ello, tomamos los índices de pobreza municipal elaborados por el Coneval, institución reconocida para la medición oficial de la pobreza, cuyos índices municipales más recientes datan de 2015. Estos índices, junto con los indicadores socioeconómicos ya expuestos, nos ofrecen un panorama más amplio de la RH2N.
3.1 El índice de pobreza multidimensional en la RHA2N
En lo que se refiere a la pobreza, de acuerdo al informe presentado por Coneval (2017a, 2017b), existían 815 mil personas en situación de pobreza multidimensional, representando un 28.8% de la población total de la RHA en estudio, valor no muy alentador, aunque cabe reconocer una disminución de 3 puntos respecto a la registrada a fines de la primera década del siglo XXI.
En el caso de la pobreza municipal, de los 78 municipios en la RHA2N en el 2010, 48 municipios, es decir, el 60%, cifra elevada, registraban un nivel de pobreza por arriba de la media de 31.9% (ANEXO 1); mientras que en 2015 se redujo la pobreza en la RH2N a 28.8% y el número de municipios en pobreza se redujo a 38, que son el 48% de los municipios, de los cuales la mayoría son rurales.
Por otra parte, la media regional de pobreza extrema fue de 3.01% en 2015, con 32 municipios arriba de la media, y el valor extremo fue en Uruachi con 42.6%. Cabe destacar que entre los 10 municipios con mayores índices de pobreza extrema, sólo 2 son urbanos y 8 son rurales; hay 4 que se ubican en la sierra baja de Chihuahua: Ocampo ,10.2% de pobreza extrema (43.7% de pobreza); Moris, 16.4% de pobreza extrema (79.2 de pobreza); Uruachi, 42.6% de pobreza extrema (86.5% de pobreza); Temósachic, 17.6% de pobreza extrema (54.6% de pobreza); y 4 en Sonora, aledaños a ellos: Yécora, que registró 18.4% de pobreza extrema (71.7% de pobreza); Quiriego, con 14.5% de pobreza extrema (61.3% de pobreza); Álamos, 10.4% de pobreza extrema (50.2% de pobreza); y Rosario, 9.3% de pobreza extrema(49.7% de pobreza).
Este análisis realizado hace prever que los municipios con elevados niveles de rezago social, de pobreza y pobreza extrema registren a su vez un bajo logro en el IPh, tal y como lo comprobaremos en este trabajo.
3.2 El índice de pobreza hídrica IPh
A continuación se sintetizan y presentan los resultados finales de la estimación del IPh para los municipios de la RHA2N, para ello se divide el conjunto de valores del IPh en cuartiles y se establecen estratos señalados por colores. Los resultados completos se muestran en los anexos 2 al 5 (Resultados del IPh municipal e indicadores de las 5 dimensiones). En los citados anexos, los valores de las dimensiones del IPh están asimismo categorizados en sus cuartiles correspondientes.
Con respecto a las características socioeconómicas y demográficas de los municipios de la RHA2N éstas se clasifican de acuerdo a los resultados del IPh y se muestran en la tabla 1. En el estrato 1, con valores de IPh muy bajos entre 0-0.583, se agrupan 20 municipios (14 rurales y 6 urbanos), que representan al 16% de la población total; de esta, 8% se encuentra en pobreza extrema. Así mismo, en el estrato 2, los valores de IPh son bajos (0.585 a 0.627) y se ubican 5 municipios urbanos y 13 rurales, que representan al 9% de la población total; de esta, el 3% son pobres extremos. En esta misma secuencia, en el estrato 3, con valores de IPh medio entre 0.627-0.657 se localizan 3 municipios urbanos y 17 rurales, cuya población representa al 10% de la población total, de la cual 4% son pobres extremos. Finalmente, en el estrato 4, con valores de IPh alto, entre 0.657 y 1, se ubican 5 municipios urbanos y 15 rurales, en los cuáles se localiza el 65% de la población total, de la cual el 4% vive en pobreza extrema.
La distribución geográfica de los estratos mencionados del IPh en los municipios de la región se muestra en la Figura 1. Por otro lado, también dejamos para el anexo todas las tablas con los cálculos intermedios para llegar al índice: Anexo 6: variables de fuentes originales, eliminación de los valores extremos y min-max; Anexo 7: variables normalizadas de las 5 dimensiones del IPh.
Figura 1 – Distribución geográfica del IPh en los municipios de la RHAN2, por cuartiles.
Fuente: elaboración propia con base en la regionalización administrativa de Conagua y la división municipal de la RHA2, Noroeste.
Cuadro 2 - Municipios que comprende la Región Hidrológico Administrativa 2 Noroeste.
Código INEGI | SONORA | 26020 | Carbó | 26040 | Nácori Chico | 26061 | Soyopa | |
26001 | Aconchi | 26021 | La Colorada | 26041 | Nacozari de García | 26062 | Suaqui Grande | |
26002 | Agua Prieta | 26022 | Cucurpe | 26042 | Navojoa | 26063 | Tepache | |
26003 | Alamos | 26023 | Cumpas | 26043 | Nogales | 26064 | Trincheras | |
26004 | Altar | 26024 | Divisaderos | 26044 | Onavas | 26065 | Tubutama | |
26005 | Arivechi | 26025 | Empalme | 26045 | Opodepe | 26066 | Ures | |
26006 | Arizpe | 26026 | Etchojoa | 26046 | Oquitoa | 26067 | Villa Hidalgo | |
26007 | Atil | 26027 | Fronteras | 26047 | Pitiquito | 26068 | Villa Pesqueira | |
26008 | Bacadéhuachi | 26028 | Granados | 26048 | Puerto Peñasco | 26069 | Yécora | |
26009 | Bacanora | 26029 | Guaymas | 26049 | Quiriego | 26070 | General Plutarco Elías Calles | |
26010 | Bacerac | 26030 | Hermosillo | 26050 | Rayón | 26071 | Benito Juárez | |
26011 | Bacoachi | 26031 | Huachinera | 26051 | Rosario | 26072 | San Ignacio Río Muerto | |
26012 | Bácum | 26032 | Huásabas | 26052 | Sahuaripa | Código INEGI | CHIHUAHUA | |
26013 | Banámichi | 26033 | Huatabampo | 26053 | San Felipe de Jesús | 8031 | Guerrero | |
26014 | Baviácora | 26034 | Huépac | 26054 | San Javier | 8040 | Madera | |
26015 | Bavispe | 26035 | Imuris | 26056 | San Miguel de Horcasitas | 8043 | Matachí | |
26016 | Benjamín Hill | 26036 | Magdalena | 26057 | San Pedro de la Cueva | 8047 | Moris | |
26017 | Caborca | 26037 | Mazatán | 26058 | Santa Ana | 8051 | Ocampo | |
26018 | Cajeme | 26038 | Moctezuma | 26059 | Santa Cruz | 8063 | Temósachi | |
26019 | Cananea | 26039 | Naco | 26060 | Sáric | 8066 | Uruachi | |
Fuente: elaboración propia, basado en la regionalización de Conagua.
4 Análisis de resultados
A continuación, se realizan comparaciones y observaciones sobre los resultados obtenidos en los indicadores de cada dimensión y del propio IPh de los municipios de la RHA2N.
A 2015, la RHA2N contaba con una población de 2,852,202 habitantes, distribuidos en 78 municipios, de los cuales 19 son urbanos (con 15,000 habitantes o más), representando al 92% de la población total. De la población total, el 29% se encontraba en pobreza moderada y el 4.2% se encontraba en pobreza extrema. En cuanto a la clasificación y características de la población de acuerdo al IPh, ésta se muestra en la Tabla 1.
El IPh de la región mostró valores desde 0.36 hasta 0.71. En ese contexto, los municipios con el IPh más bajo, menores a 0.46 resultaron ser Temósachi, Uruachi, y Etchojoa; mientras que los valores mayores a 0.70, correspondieron a los municipios de Pitiquito y Hermosillo. Los hallazgos más relevantes respecto a las características demográficas y socioeconómicas de la población, según el grado de pobreza hídrica de la tabla 1, son los siguientes: en primer lugar, se encontró que el 16% de la población total presentó un IPh muy bajo y el 9% bajo, y en cuanto a las categorías medio y alto, los porcentajes de Ph fueron de 10% y 65%, respectivamente.
Tabla 1 – Distribución y características de la población de la RHA2N al 2015 clasificada por estratos del IPh.
Estrato | 1 | 2 | 3 | 4 |
|
Rango IPh | 0 - 0.583 | 0.583 - 0.627 | 0.627 - 0.657 | 0.657 - 1 |
|
|
|
|
|
| |
Categoría | Muy bajo | Bajo | Medio | Alto | Total |
Población | 457,719 | 253,481 | 279,080 | 1,861,922 | 2,852,202 |
% Población total | 16% | 9% | 10% | 65% | 100% |
Pobres moderados | 204,485 | 87,768 | 92,024 | 439,575 | 823,852 |
% Pobres moderados | 45% | 35% | 33% | 24% | 29% |
Pobres extremos | 35,989 | 7,256 | 10,427 | 67,535 | 121,207 |
% Pobres extremos | 8% | 3% | 4% | 4% | 4% |
Municipios urbanos | 6 | 5 | 3 | 5 | 19 |
Población urbana | 379,407 | 217,579 | 230,536 | 1,795,587 | 2,623,109 |
% Población urbana | 83% | 86% | 83% | 96% | 92% |
Municipios rurales | 14 | 13 | 17 | 15 | 59 |
Población Rural | 78,312 | 35,902 | 48,544 | 66,335 | 229,093 |
% Población rural | 17% | 14% | 17% | 4% | 8% |
Municipios indígenas | 1 | - | - | - | - |
Fuente: elaboración propia con base en datos poblacionales (CONEVAL, 2017a, 2017b) y en los resultados del estudio.
4.1 Situación socioeconómica de la población en la RHA2N de acuerdo al IPh
Enseguida se examina la situación socioeconómica de la población de la región. En este sentido, se encontró que el porcentaje de pobres moderados para los estratos muy bajo y bajo fue de 45% y 35%, respectivamente, y el de pobres extremos de 8% y 3%. Bajo este mismo análisis, se encontró que la pobreza moderada en el estrato medio fue de 33% y 4% la extrema. Finalmente, en el estrato alto, los pobres moderados representaron el 24% y los pobres extremos representaron el 4%.
Hay que mencionar, además, la posición de los 19 municipios urbanos y 59 rurales dentro de los estratos del IPh. El estrato caracterizado por un IPh muy bajo comprendió 6 municipios urbanos, con el 83% de la población del estrato, y 14 municipios rurales con el 17% de dicha población. El estrato con IPh bajo incluyó 5 municipios urbanos, con el 86% de su población, y 13 rurales con el 14% de la población del estrato. Con IPh medio resultaron 3 municipios urbanos con el 83% de la población del estrato, y 17 municipios rurales con el 17% de dicha población. Finalmente, el estrato de IPh alto estuvo comprendido de 5 municipios urbanos con el 96% de la población del estrato, y de 15 municipios que sólo conformaban el 4% de la población caracterizada.
4.2 Descripción de los resultados de las dimensiones del IPh
A continuación se describen los resultados para las dimensiones acceso y capacidad del IPh. El rango de valores del indicador capacidad se presentó entre 0.251 a 0.839; mientras que para la dimensión acceso fue de 0.186 a 0.989. Por otro lado, la dimensión Recursos varió desde 0.0 hasta 0.99 y 63 municipios fueron muy bajos, lo cual muestra una gran desigualdad con los más grandes en población como Guaymas, Hermosillo y Caborca, que presentan valores de 0.73, 0.73 y 0.99, respectivamente.
En la dimensión Acceso, 49 municipios se encuentran en el rango de 0.19 a 0.96, en contraste con 8 que se encuentran en muy bajo, al sur del estado. En la dimensión Capacidad, 67 de las áreas en estudio presentan un IPh alto, con solo 2 muy bajo. El componente Uso varió de 0.19 a 0.68, con la mayoría en valor bajo y 11 en muy bajo. Por último, la dimensión Medio Ambiente E tuvo valores de 0 a 1 con mayoría de IPh medio de 33 municipios y 12 muy bajos.
También podemos comparar la relación entre los índices de pobreza IPm y el IPh. Observamos que en general los municipios con menores índices de pobreza registran los más altos IPh (más favorables). Así, Hermosillo, con índice de pobreza bajo, de 19.4 y Nogales, 23.9, con poblaciones grandes, logran IPh alto de 0.66 y 0.70, respectivamente. Por el contrario, todos los municipios de Chihuahua que forman parte de la región presentan índices de pobreza mayores de 50% junto a municipios de Sonora aledaños, como Álamos, Quiriego, Rosario y Yécora, que sufren elevada pobreza hídrica con índices que califican como bajo y muy bajo.
Por último, para comparar cuantitativamente la relación inversa entre los índices de Pm y Ph se realiza una correlación lineal y se calcula el coeficiente de correlación de Pearson r, como se muestra en las Figuras 2, 3 y 4.
El coeficiente de correlación entre ambos índices arrojó un valor de -0.67, confirmándose la suposición de que siempre que disminuya el índice de pobreza IPm, aumentará el IPh, es decir, al mejorar las dimensiones de acceso y capacidad, aumenta la satisfacción de las necesidades humanas de agua.
Figura 2 - Correlación entre los indicadores Acceso e IPh. Se muestran los coeficientes de determinación (R2) y de correlación (R) de Pearson.
Fuente: elaboración propia con base en los resultados del IPh (en anexos 2 al 5).
Figura 3 - Correlación entre los indicadores Capacidad e IPh. Se muestran los coeficientes de determinación (R2) y de correlación (R) de Pearson.
Fuente: elaboración propia con base en los resultados del IPh (anexos del 2 al 5).
Figura 4 - Correlación entre los indicadores IPm e IPh. Se muestran los coeficientes de determinación (R2) y de correlación (R) de Pearson.
Fuente: elaboración propia con base en los resultados del IPh (anexos 2 al 5).
Conclusiones
En este trabajo se implementó un índice sintético, el IPh, en una escala geográfica municipal, mucho más fina que las escalas nacionales, con el interés de hacer visible la relación entre la pobreza multidimensional y el recurso hídrico. Los municipios seleccionados conforman la Región Hidrológico Administrativa 2 Noroeste, donde diversos indicadores de desarrollo muestran logros muy favorables como promedios de la región (alta cobertura de servicios de agua, alto PIB per cápita, alta productividad agrícola e industrial entre otros), mas se consideró pertinente indagar sobre los territorios rezagados en esos avances reportados.
La capital de Sonora está en los primeros lugares, con un IPh alto, y en general los municipios con asentamientos urbanos tienen mejor desempeño, aunque poblaciones grandes como Navojoa están en menos de 60 puntos de IPh. La dimensión Capacidad mostró la mayor uniformidad en sus valores, mientras que Recursos y Ambiente fueron de mayor variabilidad, como se esperaría de una región semiárida.
La eficiencia de uso fue consistentemente baja mostrando así los probables abusos en el aprovechamiento del agua. En cuanto a la relación del IPh con la pobreza medida de manera multidimensional, Pm, se mostró en este estudio la correspondencia metodológica entre ambos índices sintéticos, observando en los resultados numéricos una correlación inversa, es decir, a una disminución de Pm se vincula una mejoría del IPh, lo que se traduce en una relativa independencia del recurso natural y medio ambiente a la hora de buscar acciones orientadas a eliminar la pobreza en todas sus formas.
En consecuencia, este estudio sugiere que el Estado, como ente rector de las políticas públicas, no deberá soslayar que el vínculo del agua con la sociedad va mucho más allá de proporcionar la infraestructura para cubrir la demanda de agua a los diferentes sectores y actores; sino que la infraestructura deberá ir acompañada, en primer lugar, de soluciones a las carencias socioeconómicas de las comunidades en los aspectos de agua y saneamiento seguro, salud, educación, e ingreso.
En ese sentido, aún cuando los alcances del IPh son limitados, su función principal es la de convencer y mostrar a los responsables de la toma de decisiones una luz sobre la orientación de las políticas públicas del agua para la población. Así, conocer su situación a escala municipal es un buen inicio, dadas las atribuciones que le otorga la constitución mexicana en el artículo 115 a los municipios en lo concerniente al manejo del agua y al saneamiento.
En síntesis, como una manera de mejorar el IPh a escala municipal, se recomienda poner en marcha políticas públicas que mejoren las capacidades de la población, tendientes a la superación de las condiciones adversas que existen o que llegaran a aparecer en la esfera de las carencias relativas a las dimensiones de la pobreza hídrica y que están vinculadas a la pobreza multidiensional, como son las abordadas en este estudio: agua y saneamiento seguro, educación, salud e ingreso.
Referências
ALKIRE, S.; FOSTER, J. Recuento y medición multidimensional de la pobreza. Oxford Poverty & Human Development Initiative (OPHI) Working Paper 7. University of Oxford. 2008.
ÁLVAREZ, Briseida, et al. Cálculo del índice de pobreza del agua en zonas semiáridas: caso Valle de San Luis Potosí. Revista Internacional de Contaminación Ambiental, v. 29, n. 4, p. 249–260. 2013.
CAMBEROS, M.; BRACAMONTES, J. El empobrecimiento de la clase media en México y en la frontera norte durante las últimas décadas del siglo XX, las políticas causales y las expectativas con la crisis actual. Cofactor. v. 1. p.23-45, 2010.
CHO, D.; OGWANG, T.; OPIO, C. Simplifying the water poverty index. Social Indicators Research, v. 97, n. 2, p. 257-267, 2010. doi: https://doi.org/10.1007/s11205-009-9501-2.
CONAGUA - COMISIÓN NACIONAL DEL AGUA. Registro Público de Derechos de Agua. 2020. Disponible en: http://sina.conagua.gob.mx/sina Consultado en: marzo 2020.
CONAGUA - COMISIÓN NACIONAL DEL AGUA. Estadísticas del agua en México: Edición 2016. Ciudad de México, México, 2016. 306 p. Disponible en: http://sina.conagua.gob.mx/publicaciones/EAM_2016.pdf Consultado en: marzo 2020.
CONEVAL - CONSEJO NACIONAL DE EVALUACIÓN DE LA POLÍTICA DE DESARROLLO SOCIAL. Metodología para la medición multidimensional de la pobreza en México. 2009. Disponible en: https://www.coneval.org.mx/Informes/Coordinacion/INFORMES_Y_PUBLICACIONES_PDF/Metodologia_Multidimensional_web.pdf Consultado en: marzo 2020.
CONEVAL - CONSEJO NACIONAL DE EVALUACIÓN DE LA POLÍTICA DraE DESARROLLO SOCIAL. Índice de Rezago Social 2015. 2017a. Disponible en: https://www.coneval.org.mx/Medicion/Documents/Pobreza_municipal/Presentacion_resultados_pobreza_municipal_2015.pdf Consultado en: febrero 2020.
CONEVAL - CONSEJO NACIONAL DE EVALUACIÓN DE LA POLÍTICA DE DESARROLLO SOCIAL. Pobreza a nivel municipio 2010 y 2015. 2017b. Disponible en: https://www.coneval.org.mx/Medicion/Paginas/Pobreza-municipal.aspx. Consultado en: febrero 2020.
FAO - FOOD AND AGRICULTURE ORGANIZATION OF THE UNITED NATIONS. AQUASTAT Main Database. 2016. Disponible en: http://www.fao.org/nr/water/aquastat/data/query/index.html?lang=en Consultado en: 19 junio 2020.
FEITELSON, E.; CHENOWETH, J. Water poverty: Towards a meaningful indicator. Water Policy, v. 4, n. 3, p. 263–281. 2002. doi: https://doi.org/10.1016/S1366-7017(02)00029-6.
HERRERA, A.; CÓRDOVA, G.; QUEVEDO, H. Incorporación de la vulnerabilidad a las inundaciones al índice de pobreza del agua en el Municipio de Juárez. CULCyT, v. 23, n. 23, p. 31–50. 2007. Disponible en http://erevistas.uacj.mx/ojs/index.php/culcyt/article/view/424/404.
INEGI - INSTITUTO NACIONAL DE ESTADÍSTICA Y GEOGRAFÍA. Anuario estadístico y geográfico de Chihuahua 2017. México, 2017. Recuperado de https://www.inegi.org.mx/app/biblioteca/ficha.html?upc=702825092139.
INEGI - INSTITUTO NACIONAL DE ESTADÍSTICA Y GEOGRAFÍA. Anuario estadístico y geográfico de Sonora 2017. 2017. Recuperado de: http://internet.contenidos.inegi.org.mx/contenidos/Productos/prod_serv/contenidos/espanol/bvinegi/productos/nueva_estruc/anuarios_2017/702825094904.pdf.
INEGI - INSTITUTO NACIONAL DE ESTADÍSTICA Y GEOGRAFÍA. Encuesta Intercensal 2015. 2015. Disponible en https://www.inegi.org.mx/programas/intercensal/2015/#Microdatos. Consultado en: marzo 2020.
INEGI - INSTITUTO NACIONAL DE ESTADÍSTICA Y GEOGRAFÍA. México en Cifras. 2020. Disponible en https://www.inegi.org.mx/app/areasgeograficas/. Consultado en: marzo 2020.
LAWRENCE, P.; MEIGH, J.; SULLIVAN, C. The Water Poverty Index : An international comparison. Keele Economics Research Papers. Keele Economics Research, v. 2002, n. 19, p. 24, 2003. Disponible en: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.536.2948&rep=rep1&type=pdf.
LISSNER, Tabea K. et al. Integrated assessments of water scarcity: knowns, unknowns and ways forward. En: BOGARDI, J. J.; BHADURI, A.; LEENTVAAR, J.; MARX, S. (Eds.), The Global Water System in the Anthropocene. Cham, Suiza. Springer International Publishing. p. 59-72. 2014.
LISTER, R. Water poverty. Journal of the Royal Society of Health. v. 115, n. 2, p. 80–83. 1995. Disponible en: https://doi.org/10.1177/146642409511500204.
MARVIN, S. J. Accessibility to utility networks: Local policy issues. Local Government Studies, v. 20, n. 3, p. 437-457. 1994. doi: https://doi.org/10.1080/03003939408433738.
MLOTE, S.; SULLIVAN, C.; MEIGH, J. Water poverty index: a tool for integrated water management. En: 3rd Waternet /Warfsa Symposium "Water Demand Management For Sustainable Development". Dar es Salaam, 30-31 octubre 2002. 2002.
MOLLE, F.; MOLLINGA, P. Water poverty indicators: Conceptual problems and policy issues. Water Policy. v. 5, n. 5, p. 529-544, 2003. doi: https://doi.org/10.2166/wp.2003.0034.
MOLLE, F.; MOLLINGA, P.; MEINZEN-DICK, R. Water, politics and development: Introducing water alternatives. Water alternatives. v. 1, n. 1, p. 1-6, 2008. Disponible en: http://www.water-alternatives.org/index.php/allabs/14-a-1-1-1/file.
NARDO, M., SAISANA, M., SALTELLI, A., TARANTOLA, S., HOFFMAN, A., y GIOVANNINI, E. Handbook on constructing composite indicators and user guide. OECD Publishing. Paris, France. 162p. 2008. doi: https://doi.org/10.1787/18152031.
ONU - ORGANIZACIÓN DE LAS NACIONES UNIDAS. Resolución 70/1 de la Asamblea General Transformar nuestro mundo: la Agenda 2030 para el Desarrollo Sostenible. Organización de las Naciones Unidas. 2015. Recuperado de: https://undocs.org/sp/A/RES/70/1 Consultado en: marzo 2019.
PÉREZ-FOGUET, A.; GINÉ-GARRIGA, R. Analyzing Water Poverty in Basins. Water Resources Management, v. 25, n. 14, p. 3595–3612. 2011. doi: https://doi.org/10.1007/s11269-011-9872-4.
PIGOU, A. C. The Economics of Welfare. 4a ed. Macmillan. London, UK. 550 p., 1932.
PNUD - PROGRAMA DE LAS NACIONES UNIDAS PARA EL DESARROLLO. Informe sobre desarrollo humano 2016. Recuperado de: http://hdr.undp.org/sites/default/files/HDR2016_SP_Overview_Web.pdf Consultado en: 23 oct. 2018.
PNUD - PROGRAMA DE LAS NACIONES UNIDAS PARA EL DESARROLLO. Objetivos del Desarrollo Sostenible. Objetivo 6: Agua limpia y saneamiento. 2019a. Recuperado de https://www.undp.org/content/undp/es/home/sustainable-development-goals/goal-6-clean-water-and-sanitation.html Consultado en: 14 mar. 2019.
PNUD - PROGRAMA DE LAS NACIONES UNIDAS PARA EL DESARROLLO. Informe de Desarrollo Humano Municipal 2010-2015. Transformando México desde lo local. 2019b. Recuperado de: https://www.mx.undp.org/content/mexico/es/home/library/poverty/informe-de-desarrollo-humano-municipal-2010-2015--transformando-.html Consultado en: marzo 2020.
RIJSBERMAN, F. R. Water scarcity: Fact or fiction? Agricultural Water Management, v. 80, n. 1-3, p. 5-22. 2006. doi: 10.1016/j.agwat.2005.07.001.
SEMARNAT - SECRETARIA DE MEDIO AMBIENTE Y RECURSOS NATURALES. Sistema de Información Geográfica para la Evaluación del Impacto Ambiental. 2020. Disponible en: https://mapas.semarnat.gob.mx/sigeia/#/sigeia. Consultado en: marzo 2020.
SEN, A. Capability and Wellbeing. En: NUSSBAUM, M.; SEN, A. (Ed.), The Quality of Life. Oxford, UK: Clarendon Press. p. 30-53, 1993.
SEN, Amartya. Poverty: An ordinal Approach to measurement. Econometrica: Journal of Econometric Society. v. .44, n. 2, p. 219-231. 1976.
SULLIVAN, C.; MEIGH, J.; LAWRENCE, P. Application of the Water Poverty Index at different scales: A cautionary tale: In Memory of Jeremy Meigh who gaves his life´s work to the improvement of peoples lives. Water International, v. 31, n. 3, p. 412-426. 2006 doi: https://doi.org/10.1080/02508060608691942.
SULLIVAN, C. The Potential for Calculating a Meaningful Water Poverty Index, Water International, v. 26, n. 4, p. 471-480, 2001. doi: https://doi.org/10.1080/02508060108686948.
SULLIVAN, C.; MEIGH, J. Considering the Water Poverty Index in the context of poverty alleviation. Water Policy. v. 1 October 2003, n. 5-6, p. 513–528. 2003. doi: https://doi.org/10.2166/wp.2003.0033.
TOWNSEND, P. Poverty in the United Kingdom: A survey of household resources and standards of living. University of California Press, 1216 p, 1979.
WRI - WORLD RESOURCES INSTITUTE. Global Forest Watch. 2020. Disponible en: https://www.globalforestwatch.org/map?. Consultado en: marzo 2020.
María Juliana Olivas-Palma Doctorante en Desarrollo Regional en el Centro de Investigación en Alimentación y Desarrollo A.C. Hermosillo, Sonora, México; Maestra en Ciencias de la Ingeniería Industrial (2013) por la Universidad de Sonora, México; Ingeniera Industrial en Electrónica (2005), por el Instituto Tecnológico Nacional de México, en Hermosillo, Sonora, México. Áreas de interés: Desarrollo humano, Desarrollo regional, Políticas públicas, Pobreza, Bienestar y Desigualdad. ORCID: https://orcid.org/0000-0002-7704-260X Mario Camberos-Castro Dr. en Ciencias Económicas, por la Universidad Autónoma de Baja California, Tijuana, México; Maestro en Ciencias Económicas por la Universidad Nacional Autónoma de México; Licenciado en Economía por la Universidad de Guadalajara, México; Investigador titular “E” en Centro de Investigación y Desarrollo A.C. (CIAD), Dpto. de Economía; Miembro del Sistema Nacional de Investigadores, Nivel II; Profesor investigador emérito del CIAD, Miembro de la Academia Mexicana de Ciencias (AMCE); Evaluador del Consejo Nacional para la Acreditación de las Ciencias Económicas. Líneas de investigación: Política económica, Bienestar, Desigualdad, Pobreza, Mercados laborales y Evaluación de Políticas Sociales. |
ANEXOS
Anexo 1 – Pobreza multidimensional en municipios que incluye la Región Hidrológico Administrativa 2 Noroeste, de México, en los años 2010 y 2015.
Código Inegi | Municipio | Población | Porcentaje de población en situación de pobreza | Número de personas en situación de pobreza | Porcentaje de población en situación de pobreza extrema | Número de personas en situación de pobreza extrema | |||||
2010 | 2015 | 2010 | 2015 | 2010 | 2015 | 2010 | 2015 | 2010 | 2015 | ||
08031 | Guerrero | 37,869 | 39,916 | 49.8 | 50.2 | 18,842 | 20,020 | 8.9 | 4.6 | 3,365 | 1,856 |
08040 | Madera | 35,770 | 29,848 | 65.4 | 49.9 | 23,402 | 14,899 | 14.2 | 3.6 | 5,090 | 1,073 |
08043 | Matachí | 3,078 | 3,101 | 40.5 | 44.9 | 1,246 | 1,394 | 4.6 | 5.1 | 142 | 159 |
08047 | Moris | 5,308 | 5,384 | 72.2 | 79.2 | 3,833 | 4,264 | 27.2 | 16.4 | 1,442 | 884 |
08051 | Ocampo | 7,326 | 7,925 | 54.1 | 43.7 | 3,964 | 3,460 | 20.3 | 10.2 | 1,485 | 811 |
08063 | Temósachic* | 6,266 | 6,266 | 54.6 | 54.6 | 3,419 | 3,419 | 17.6 | 17.6 | 1,101 | 1,101 |
08066 | Uruachi | 8,224 | 6,382 | 86.0 | 86.5 | 7,071 | 5,523 | 43.2 | 42.6 | 3,554 | 2,717 |
26001 | Aconchi | 2,637 | 2,862 | 29.9 | 19.7 | 787 | 563 | 2.2 | 1.7 | 58 | 48 |
26002 | Agua Prieta | 80,103 | 87,269 | 36.2 | 33.1 | 29,013 | 28,926 | 4.2 | 2.6 | 3,338 | 2,264 |
26003 | Alamos | 27,503 | 24,054 | 64.3 | 50.2 | 17,674 | 12,080 | 20.2 | 10.4 | 5,569 | 2,497 |
26004 | Altar | 9,672 | 9,956 | 47.4 | 46.9 | 4,585 | 4,671 | 5.7 | 4.1 | 555 | 404 |
26005 | Arivechi | 1,219 | 1,209 | 30.4 | 26.4 | 370 | 319 | 4.1 | 6.5 | 50 | 79 |
26006 | Arizpe | 3,027 | 2,783 | 25.5 | 26.1 | 772 | 725 | 1.3 | 1.1 | 39 | 32 |
26007 | Atil | 624 | 604 | 23.3 | 4.1 | 145 | 25 | 0.7 | 0.1 | 5 | 1 |
26008 | Bacadéhuachi | 1,251 | 1,126 | 38.5 | 34.2 | 481 | 385 | 5.9 | 3.9 | 73 | 44 |
26009 | Bacanora | 781 | 833 | 45.4 | 14.0 | 354 | 117 | 5.6 | 1.1 | 44 | 9 |
26010 | Bacerac | 1,464 | 1,421 | 43.0 | 43.8 | 630 | 623 | 7.8 | 5.4 | 114 | 77 |
26011 | Bacoachi | 1,633 | 1,613 | 30.4 | 34.4 | 497 | 555 | 1.5 | 2.5 | 25 | 40 |
26012 | Bácum | 23,887 | 22,520 | 44.7 | 46.3 | 10,666 | 10,421 | 6.9 | 6.6 | 1,647 | 1,489 |
26013 | Banámichi | 1,633 | 1,675 | 32.5 | 22.2 | 531 | 371 | 1.8 | 0.6 | 29 | 11 |
26014 | Baviácora | 3,542 | 3,443 | 30.3 | 15.4 | 1,072 | 531 | 1.5 | 0.7 | 53 | 25 |
26015 | Bavispe | 1,449 | 1,513 | 37.2 | 45.5 | 540 | 688 | 2.0 | 3.5 | 29 | 53 |
26016 | Benjamín Hill | 5,492 | 5,441 | 35.9 | 31.2 | 1,972 | 1,698 | 5.1 | 2.3 | 279 | 126 |
26017 | Caborca | 79,312 | 89,457 | 31.7 | 31.6 | 25,159 | 28,230 | 3.7 | 3.1 | 2,921 | 2,768 |
26018 | Cajeme | 410,005 | 445,700 | 27.7 | 28.8 | 113,422 | 128,158 | 2.9 | 2.0 | 11,712 | 8,935 |
26019 | Cananea | 36,140 | 36,378 | 36.3 | 26.1 | 13,115 | 9,480 | 2.0 | 0.8 | 729 | 309 |
26020 | Carbó | 3,495 | 5,031 | 51.2 | 42.3 | 1,791 | 2,129 | 9.6 | 4.6 | 335 | 231 |
26021 | La Colorada | 1,638 | 2,156 | 21.4 | 23.6 | 350 | 509 | 1.7 | 2.4 | 28 | 52 |
26022 | Cucurpe | 948 | 1,002 | 39.0 | 19.1 | 369 | 191 | 4.1 | 0.9 | 39 | 9 |
26023 | Cumpas | 5,786 | 6,351 | 25.9 | 22.9 | 1,496 | 1,454 | 1.2 | 0.8 | 69 | 49 |
26024 | Divisaderos | 813 | 744 | 35.8 | 22.7 | 291 | 169 | 3.0 | 1.5 | 25 | 11 |
26025 | Empalme | 56,137 | 59,340 | 36.4 | 28.3 | 20,443 | 16,797 | 5.4 | 2.3 | 3,024 | 1,370 |
26026 | Etchojoa | 64,540 | 59,880 | 57.8 | 50.2 | 37,292 | 30,073 | 16.3 | 11.4 | 10,509 | 6,813 |
26027 | Fronteras | 9,377 | 9,007 | 32.1 | 24.1 | 3,007 | 2,169 | 5.1 | 2.0 | 478 | 180 |
26028 | Granados | 1,150 | 1,104 | 27.2 | 8.7 | 312 | 96 | 1.0 | 0.1 | 12 | 1 |
26029 | Guaymas | 157,049 | 168,456 | 29.4 | 30.7 | 46,129 | 51,723 | 5.4 | 4.3 | 8,450 | 7,263 |
26030 | Hermosillo | 806,063 | 923,631 | 25.4 | 19.4 | 205,006 | 179,475 | 3.3 | 1.4 | 26,227 | 12,677 |
26031 | Huachinera | 1,350 | 1,277 | 31.5 | 30.0 | 425 | 383 | 4.2 | 2.9 | 57 | 37 |
26032 | Huásabas | 962 | 923 | 51.5 | 11.7 | 495 | 108 | 4.0 | 0.1 | 38 | 1 |
26033 | Huatabampo | 94,049 | 82,593 | 53.3 | 46.3 | 50,173 | 38,207 | 12.4 | 7.5 | 11,649 | 6,192 |
26034 | Huépac | 1,149 | 963 | 16.5 | 2.7 | 190 | 26 | 0.3 | 0.0 | 4 | 0 |
26035 | Imuris | 11,675 | 13,094 | 42.2 | 27.9 | 4,928 | 3,652 | 5.8 | 1.7 | 680 | 226 |
26036 | Magdalena | 31,598 | 32,232 | 33.6 | 28.9 | 10,609 | 9,330 | 3.2 | 1.5 | 998 | 485 |
26037 | Mazatán | 1,314 | 1,286 | 20.4 | 19.5 | 268 | 250 | 1.0 | 0.8 | 13 | 11 |
26038 | Moctezuma | 5,836 | 5,163 | 26.4 | 22.3 | 1,540 | 1,151 | 1.9 | 0.6 | 109 | 32 |
26039 | Naco | 6,063 | 6,404 | 53.5 | 30.6 | 3,243 | 1,960 | 6.4 | 2.0 | 388 | 128 |
26040 | Nácori Chico | 2,044 | 2,097 | 59.0 | 61.0 | 1,205 | 1,280 | 11.1 | 9.3 | 226 | 195 |
26041 | Nacozari de García | 10,428 | 13,961 | 20.9 | 15.7 | 2,177 | 2,193 | 2.0 | 0.9 | 203 | 123 |
26042 | Navojoa | 185,237 | 167,950 | 42.4 | 36.2 | 78,628 | 60,868 | 8.0 | 4.2 | 14,870 | 7,075 |
26043 | Nogales | 224,113 | 249,530 | 30.5 | 23.9 | 68,429 | 59,617 | 4.5 | 1.7 | 10,153 | 4,349 |
26044 | Onavas | 393 | 487 | 28.6 | 5.7 | 112 | 28 | 3.0 | 0.2 | 12 | 1 |
26045 | Opodepe | 2,863 | 2,747 | 46.4 | 30.0 | 1,328 | 823 | 10.0 | 3.9 | 286 | 107 |
26046 | Oquitoa | 439 | 387 | 16.9 | 4.7 | 74 | 18 | 1.3 | 0.3 | 6 | 1 |
26047 | Pitiquito | 8,228 | 9,889 | 32.4 | 27.1 | 2,668 | 2,675 | 4.4 | 2.8 | 359 | 274 |
26048 | Puerto Peñasco | 54,222 | 65,105 | 41.6 | 39.8 | 22,551 | 25,898 | 6.1 | 3.9 | 3,306 | 2,558 |
26049 | Quiriego | 3,338 | 2,947 | 47.5 | 61.3 | 1,586 | 1,806 | 16.1 | 14.5 | 536 | 427 |
26050 | Rayón | 1,598 | 1,499 | 37.2 | 30.9 | 594 | 463 | 4.0 | 2.3 | 64 | 35 |
26051 | Rosario | 5,098 | 5,223 | 51.9 | 49.7 | 2,645 | 2,596 | 12.0 | 9.3 | 613 | 487 |
26052 | Sahuaripa | 5,940 | 5,849 | 45.7 | 40.1 | 2,715 | 2,348 | 7.3 | 4.5 | 432 | 266 |
26053 | San Felipe de Jesús | 394 | 423 | 25.2 | 4.3 | 99 | 18 | 1.3 | 0.0 | 5 | 0 |
26054 | San Javier | 483 | 579 | 5.2 | 5.9 | 25 | 34 | 0.7 | 0.3 | 3 | 2 |
26056 | San Miguel de Horcasitas | 7,733 | 9,441 | 62.3 | 48.4 | 4,816 | 4,570 | 24.5 | 10.4 | 1,895 | 981 |
26057 | San Pedro de la Cueva | 1,601 | 1,540 | 29.0 | 17.9 | 464 | 275 | 3.1 | 1.6 | 49 | 25 |
26058 | Santa Ana | 14,945 | 16,840 | 35.0 | 25.6 | 5,226 | 4,313 | 2.2 | 1.3 | 324 | 223 |
26059 | Santa Cruz | 1,945 | 1,833 | 30.2 | 35.1 | 586 | 643 | 3.5 | 3.0 | 68 | 54 |
26060 | Sáric | 2,674 | 1,629 | 24.9 | 27.4 | 667 | 446 | 2.6 | 3.2 | 69 | 52 |
26061 | Soyopa | 1,278 | 1,474 | 20.0 | 23.8 | 256 | 350 | 1.0 | 3.0 | 12 | 44 |
26062 | Suaqui Grande | 1,118 | 1,187 | 29.5 | 11.8 | 330 | 140 | 2.2 | 0.7 | 24 | 8 |
26063 | Tepache | 1,365 | 1,279 | 37.2 | 15.6 | 508 | 200 | 4.1 | 0.6 | 56 | 8 |
26064 | Trincheras | 1,713 | 1,635 | 35.8 | 22.0 | 613 | 360 | 4.6 | 2.1 | 79 | 34 |
26065 | Tubutama | 1,730 | 1,240 | 26.0 | 22.3 | 450 | 276 | 1.7 | 1.1 | 29 | 14 |
26066 | Ures | 8,274 | 9,047 | 32.9 | 18.6 | 2,720 | 1,686 | 2.4 | 0.7 | 202 | 65 |
26067 | Villa Hidalgo | 1,737 | 1,581 | 15.9 | 19.9 | 277 | 314 | 0.8 | 0.9 | 14 | 15 |
26068 | Villa Pesqueira | 1,254 | 1,228 | 35.4 | 38.4 | 443 | 472 | 1.9 | 1.7 | 24 | 21 |
26069 | Yécora | 6,256 | 6,239 | 70.2 | 71.7 | 4,391 | 4,474 | 29.3 | 18.4 | 1,832 | 1,145 |
26070 | Plutarco E.C* | 11,125 | 11,125 | 49.0 | 49.0 | 5,448 | 5,448 | 9.0 | 9.0 | 997 | 997 |
26071 | Benito Juárez | 20,613 | 22,410 | 51.7 | 43.3 | 10,656 | 9,713 | 12.9 | 5.1 | 2,651 | 1,144 |
26072 | San Ignacio Río Muerto | 16,271 | 14,485 | 54.5 | 56.0 | 8,863 | 8,108 | 14.0 | 10.6 | 2,271 | 1,531 |
*2015 no tiene datos disponibles, por lo que se estiman con los datos de 2010. | |||||||||||
Población | 2,662,657 | 2,852,202 | 903,469 | 823,850 | 148,250 | 85,841 | |||||
Promedio de la región | 33.93% | 28.88% | 5.57% | 3.01% | |||||||
Variación respecto a 2010 | -5.0% | -2.6% | |||||||||
Municipios en pobreza mayor al promedio | 43 | 39 | 29 | 32 | |||||||
Fracción del número de municipios | 55% | 50% | 37% | 41% | |||||||
Urbano | 19 | 19 | |||||||||
Rural |
| 59 | 59 |
|
|
|
|
|
|
|
|
Fuente: elaboración propia en base a Coneval (2017a, 2017b).
Anexo 2 – IPh municipal e indicadores de las 5 dimensiones, estrato 1, muy bajo.
Clave | Municipio | R | A | C | U | E | IPh |
26026 | Etchojoa | 0.02 | 0.43 | 0.73 | 0.64 | 0 | 0.36 |
8066 | Uruachi | 0.41 | 0.19 | 0.58 | 0.17 | 0.63 | 0.4 |
8063 | Temósachi | 0.47 | 0.61 | 0.25 | 0.5 | 0.46 | 0.46 |
26072 | San Ignacio Río Muerto | 0.19 | 0.44 | 0.73 | 0.58 | 0.45 | 0.48 |
26003 | Alamos | 0.46 | 0.37 | 0.71 | 0.58 | 0.3 | 0.48 |
26049 | Quiriego | 0.45 | 0.46 | 0.64 | 0.52 | 0.36 | 0.49 |
26071 | Benito Juárez | 0 | 0.65 | 0.75 | 0.62 | 0.45 | 0.49 |
8047 | Moris | 0.38 | 0.27 | 0.62 | 0.19 | 1 | 0.49 |
26069 | Yécora | 0.42 | 0.42 | 0.66 | 0.29 | 0.68 | 0.5 |
26012 | Bácum | 0.27 | 0.71 | 0.73 | 0.64 | 0.12 | 0.5 |
26061 | Soyopa | 0.35 | 0.54 | 0.7 | 0.21 | 0.71 | 0.5 |
26033 | Huatabampo | 0.23 | 0.43 | 0.76 | 0.66 | 0.45 | 0.51 |
8051 | Ocampo | 0.38 | 0.37 | 0.67 | 0.2 | 1 | 0.53 |
26070 | General Plutarco E. Calles | 0.44 | 0.8 | 0.29 | 0.57 | 0.67 | 0.55 |
26042 | Navojoa | 0.38 | 0.68 | 0.79 | 0.57 | 0.38 | 0.56 |
26056 | San Miguel de Horcasitas | 0.31 | 0.55 | 0.67 | 0.64 | 0.67 | 0.57 |
26021 | La Colorada | 0.46 | 0.66 | 0.72 | 0.47 | 0.57 | 0.58 |
26065 | Tubutama | 0.38 | 0.59 | 0.71 | 0.56 | 0.67 | 0.58 |
26011 | Bacoachi | 0.36 | 0.75 | 0.74 | 0.5 | 0.56 | 0.58 |
26064 | Trincheras | 0.41 | 0.65 | 0.72 | 0.47 | 0.67 | 0.58 |
Fuente: elaboración propia.
Anexo 3 – Resultados del IPh municipal e indicadores de las 5 dimensiones estrato 2, bajo.
Clave | Municipio | R | A | C | U | E | IPh |
26035 | Imuris | 0.39 | 0.66 | 0.77 | 0.55 | 0.57 | 0.59 |
8031 | Guerrero | 0.51 | 0.61 | 0.71 | 0.52 | 0.62 | 0.59 |
26059 | Santa Cruz | 0.35 | 0.69 | 0.73 | 0.53 | 0.67 | 0.59 |
26045 | Opodepe | 0.39 | 0.65 | 0.71 | 0.54 | 0.67 | 0.59 |
26057 | San Pedro de la Cueva | 0.4 | 0.75 | 0.73 | 0.47 | 0.62 | 0.6 |
26010 | Bacerac | 0.37 | 0.57 | 0.69 | 0.57 | 0.78 | 0.6 |
26054 | San Javier | 0.34 | 0.67 | 0.77 | 0.42 | 0.8 | 0.6 |
26025 | Empalme | 0.3 | 0.73 | 0.79 | 0.64 | 0.56 | 0.6 |
26015 | Bavispe | 0.38 | 0.6 | 0.71 | 0.62 | 0.71 | 0.6 |
26058 | Santa Ana | 0.35 | 0.86 | 0.79 | 0.47 | 0.56 | 0.61 |
26016 | Benjamín Hill | 0.37 | 0.93 | 0.77 | 0.41 | 0.56 | 0.61 |
8043 | Matachí | 0.34 | 0.68 | 0.71 | 0.62 | 0.71 | 0.61 |
26008 | Bacadéhuachi | 0.36 | 0.75 | 0.71 | 0.54 | 0.73 | 0.62 |
26031 | Huachinera | 0.36 | 0.66 | 0.73 | 0.57 | 0.78 | 0.62 |
26048 | Puerto Peñasco | 0.57 | 0.79 | 0.79 | 0.39 | 0.56 | 0.62 |
26019 | Cananea | 0.39 | 0.95 | 0.82 | 0.37 | 0.56 | 0.62 |
26022 | Cucurpe | 0.37 | 0.76 | 0.72 | 0.58 | 0.67 | 0.62 |
26068 | Villa Pesqueira | 0.36 | 0.86 | 0.72 | 0.49 | 0.7 | 0.62 |
26006 | Arizpe | 0.43 | 0.86 | 0.74 | 0.54 | 0.57 | 0.63 |
Fuente: elaboración propia.
Anexo 4 – Resultados del IPh municipal e indicadores de las 5 dimensiones estrato 3, medio.
Clave | Municipio | R | A | C | U | E | IPh |
26014 | Baviácora | 0.34 | 0.78 | 0.76 | 0.58 | 0.68 | 0.63 |
26036 | Magdalena | 0.39 | 0.92 | 0.8 | 0.48 | 0.56 | 0.63 |
26060 | Sáric | 0.36 | 0.81 | 0.72 | 0.59 | 0.67 | 0.63 |
26040 | Nácori Chico | 0.42 | 0.63 | 0.67 | 0.57 | 0.88 | 0.63 |
26062 | Suaqui Grande | 0.35 | 0.96 | 0.74 | 0.51 | 0.61 | 0.63 |
26037 | Mazatán | 0.34 | 0.94 | 0.76 | 0.45 | 0.67 | 0.63 |
26051 | Rosario | 0.45 | 0.6 | 0.69 | 0.56 | 0.89 | 0.64 |
26050 | Rayón | 0.34 | 0.85 | 0.71 | 0.6 | 0.68 | 0.64 |
26009 | Bacanora | 0.36 | 0.85 | 0.73 | 0.53 | 0.72 | 0.64 |
26029 | Guaymas | 0.73 | 0.76 | 0.79 | 0.67 | 0.25 | 0.64 |
26004 | Altar | 0.47 | 0.8 | 0.75 | 0.64 | 0.56 | 0.64 |
26023 | Cumpas | 0.39 | 0.79 | 0.78 | 0.58 | 0.68 | 0.64 |
26044 | Onavas | 0.34 | 0.83 | 0.74 | 0.54 | 0.77 | 0.65 |
8040 | Madera | 0.65 | 0.66 | 0.71 | 0.53 | 0.68 | 0.65 |
26020 | Carbó | 0.41 | 0.9 | 0.74 | 0.66 | 0.56 | 0.65 |
26063 | Tepache | 0.35 | 0.9 | 0.76 | 0.55 | 0.7 | 0.65 |
26013 | Banámichi | 0.34 | 0.96 | 0.75 | 0.53 | 0.68 | 0.65 |
26001 | Aconchi | 0.32 | 0.88 | 0.75 | 0.63 | 0.68 | 0.65 |
26032 | Huásabas | 0.34 | 0.97 | 0.77 | 0.62 | 0.57 | 0.65 |
Fuente: elaboración propia.
Anexo 5 – Resultados del IPh municipal e indicadores de las 5 dimensiones estrato 4, alto.
Clave | Municipio | R | A | C | U | E | IPh |
26039 | Naco | 0.37 | 0.93 | 0.78 | 0.53 | 0.67 | 0.66 |
26066 | Ures | 0.42 | 0.89 | 0.77 | 0.65 | 0.57 | 0.66 |
26043 | Nogales | 0.7 | 0.88 | 0.82 | 0.46 | 0.45 | 0.66 |
26017 | Caborca | 0.99 | 0.76 | 0.77 | 0.56 | 0.22 | 0.66 |
26005 | Arivechi | 0.34 | 0.93 | 0.73 | 0.49 | 0.82 | 0.66 |
26046 | Oquitoa | 0.35 | 0.97 | 0.77 | 0.56 | 0.67 | 0.66 |
26007 | Atil | 0.33 | 0.96 | 0.79 | 0.58 | 0.67 | 0.67 |
26024 | Divisaderos | 0.34 | 0.96 | 0.76 | 0.59 | 0.68 | 0.67 |
26067 | Villa Hidalgo | 0.35 | 0.92 | 0.75 | 0.64 | 0.68 | 0.67 |
26034 | Huépac | 0.32 | 0.97 | 0.81 | 0.57 | 0.67 | 0.67 |
26052 | Sahuaripa | 0.5 | 0.87 | 0.73 | 0.53 | 0.71 | 0.67 |
26041 | Nacozari de García | 0.38 | 0.92 | 0.81 | 0.57 | 0.68 | 0.67 |
26002 | Agua Prieta | 0.56 | 0.9 | 0.79 | 0.55 | 0.57 | 0.67 |
26028 | Granados | 0.32 | 0.99 | 0.79 | 0.63 | 0.68 | 0.68 |
26038 | Moctezuma | 0.39 | 0.96 | 0.82 | 0.66 | 0.58 | 0.68 |
26053 | San Felipe de Jesús | 0.33 | 0.99 | 0.78 | 0.62 | 0.69 | 0.68 |
26018 | Cajeme | 0.51 | 0.94 | 0.81 | 0.56 | 0.6 | 0.68 |
26027 | Fronteras | 0.4 | 0.92 | 0.79 | 0.68 | 0.67 | 0.69 |
26030 | Hermosillo | 0.73 | 0.93 | 0.84 | 0.46 | 0.56 | 0.7 |
26047 | Pitiquito | 0.66 | 0.77 | 0.77 | 0.68 | 0.67 | 0.71 |
Fuente: elaboración propia.
Anexo 6 – Variables de fuentes originales, eliminación de extremos y Min-Max.
ID | 1r. | 2r. | 3r. | 1ª. | 2ª. | 3ª. | 4ª. | 1u. | 2u. | 3u. | 4u. | 5u. | 1e. | 2e. | 3e. |
8031 | 241.0 | 37.0 | 0.65 | 0.74 | 0.93 | 0.66 | 0.79 | 9.13 | 640.3 | 146.3 | 0.64 | 0.00 | M | 6.90 | no |
8040 | 369.3 | 49.6 | 0.05 | 0.76 | 0.96 | 0.76 | 0.77 | 4.74 | 443.9 | 13.4 | 0.13 | 0.00 | A | 27.00 | no |
8043 | 29.7 | 4.4 | 0.12 | 0.77 | 0.99 | 0.68 | 0.88 | 0.24 | 222.1 | 3.2 | 0.00 | 0.00 | B | 4.50 | no |
8047 | 76.1 | 1.8 | 0.03 | 0.38 | 0.91 | 0.27 | 0.76 | 1.89 | 1008.3 | 0.0 | 0.19 | 0.00 | B | 38.00 | no |
8051 | 76.3 | 0.5 | 0.04 | 0.52 | 0.92 | 0.45 | 0.58 | 2.60 | 941.5 | 0.0 | 0.50 | 0.00 | B | 46.00 | no |
8063 | 180.1 | 5.7 | 0.02 | 0.74 | 0.93 | 0.66 | 0.79 | 1.00 | 424.7 | 3.4 | 0.00 | 0.00 | B | 14.00 | si |
8066 | 112.0 | 0.9 | 0.02 | 0.27 | 0.73 | 0.43 | 0.40 | 2.53 | 1138.8 | 0.0 | 0.00 | 0.00 | B | 34.00 | si |
26001 | 15.5 | 6.1 | 0.44 | 0.99 | 0.99 | 0.80 | 0.98 | 0.29 | 289.3 | 6.5 | 0.04 | 0.00 | B | 1.70 | no |
26002 | 166.2 | 202.0 | 0.20 | 0.95 | 0.99 | 0.87 | 0.99 | 3.22 | 106.4 | 20.4 | 10.14 | 0.00 | M | 1.90 | no |
26003 | 270.8 | 20.0 | 2.28 | 0.42 | 0.92 | 0.56 | 0.62 | 3.29 | 351.2 | 605.5 | 9.61 | 0.00 | AA | 34.00 | si |
26004 | 187.7 | 6.0 | 0.35 | 0.86 | 0.98 | 0.78 | 0.96 | 0.98 | 281.2 | 64.0 | 1.38 | 0.00 | M | 0.03 | no |
26005 | 27.9 | 1.6 | 0.06 | 0.97 | 0.99 | 0.93 | 0.95 | 0.25 | 591.3 | 1.3 | 0.00 | 0.00 | B | 18.00 | no |
26006 | 129.5 | 6.6 | 0.09 | 0.96 | 1.00 | 0.77 | 0.99 | 0.58 | 592.6 | 11.3 | 0.00 | 0.00 | M | 1.10 | no |
26007 | 12.6 | 1.6 | 0.19 | 0.95 | 1.00 | 0.99 | 0.99 | 0.11 | 503.7 | 2.3 | 0.00 | 0.00 | B | 0.04 | no |
26008 | 44.9 | 3.3 | 0.00 | 0.92 | 0.99 | 0.61 | 0.94 | 0.09 | 217.6 | 0.1 | 0.00 | 0.00 | B | 7.20 | no |
26009 | 47.7 | 0.0 | 0.05 | 0.93 | 0.99 | 0.82 | 0.96 | 0.16 | 550.0 | 2.3 | 0.00 | 0.00 | M | 19.00 | no |
26010 | 56.6 | 0.0 | 0.06 | 0.83 | 0.98 | 0.40 | 0.84 | 0.19 | 372.8 | 3.3 | 0.00 | 0.00 | B | 13.00 | no |
26011 | 51.9 | 2.4 | 0.04 | 0.97 | 0.99 | 0.56 | 0.98 | 0.41 | 722.8 | 1.9 | 0.00 | 0.00 | M | 0.29 | no |
26012 | 66.5 | 0.0 | 2.64 | 0.73 | 0.98 | 0.85 | 0.84 | 2.00 | 237.3 | 173.4 | 0.20 | 0.00 | A | 1.40 | si |
26013 | 34.0 | 4.9 | 0.30 | 0.99 | 1.00 | 0.93 | 0.99 | 0.36 | 616.9 | 9.5 | 0.29 | 0.00 | B | 1.60 | no |
26014 | 35.5 | 7.0 | 0.34 | 0.98 | 0.99 | 0.60 | 0.99 | 0.60 | 492.2 | 11.4 | 0.00 | 0.00 | B | 1.20 | no |
26015 | 72.6 | 5.2 | 0.17 | 0.94 | 0.99 | 0.26 | 0.99 | 0.19 | 351.6 | 11.8 | 0.00 | 0.00 | B | 5.00 | no |
26016 | 59.4 | 13.9 | 0.24 | 0.96 | 0.99 | 0.95 | 0.96 | 2.08 | 1088.5 | 12.0 | 0.00 | 0.00 | M | 0.00 | no |
26017 | 452.5 | 644.5 | 0.15 | 0.80 | 0.98 | 0.79 | 0.92 | 8.28 | 264.8 | 51.3 | 9.32 | 0.00 | M | 0.05 | si |
26018 | 205.7 | 1219.8 | 7.89 | 0.95 | 0.99 | 0.97 | 0.97 | 100.46 | 635.5 | 1517.9 | 5.69 | 0.00 | M | 5.50 | no |
26019 | 97.4 | 23.2 | 0.65 | 0.98 | 1.00 | 0.94 | 0.99 | 7.44 | 568.2 | 28.8 | 27.20 | 0.00 | M | 0.97 | no |
26020 | 108.9 | 11.6 | 0.29 | 0.93 | 0.99 | 0.92 | 0.95 | 0.31 | 176.0 | 30.7 | 0.00 | 0.00 | M | 0.04 | no |
26021 | 173.7 | 2.6 | 0.09 | 0.72 | 0.98 | 0.65 | 0.94 | 0.57 | 757.5 | 14.7 | 0.91 | 0.00 | M | 1.90 | no |
26022 | 66.1 | 1.6 | 0.07 | 0.94 | 0.96 | 0.64 | 0.97 | 0.14 | 400.3 | 4.6 | 0.00 | 0.00 | B | 0.61 | no |
26023 | 84.7 | 6.7 | 0.22 | 0.96 | 0.99 | 0.65 | 0.98 | 0.91 | 406.8 | 16.3 | 1.27 | 0.00 | B | 1.50 | no |
26024 | 16.6 | 2.3 | 0.02 | 0.96 | 0.99 | 0.99 | 0.98 | 0.07 | 282.8 | 0.3 | 0.00 | 0.00 | B | 2.00 | no |
26025 | 25.0 | 83.2 | 2.20 | 0.74 | 0.97 | 0.78 | 0.96 | 5.25 | 256.2 | 49.8 | 0.01 | 0.00 | M | 0.09 | no |
26026 | 40.0 | 0.0 | 13.54 | 0.51 | 0.96 | 0.76 | 0.49 | 4.37 | 189.3 | 537.3 | 0.26 | 0.00 | AA | 0.07 | si |
26027 | 110.6 | 1.8 | 0.24 | 0.95 | 0.99 | 0.92 | 0.97 | 0.55 | 172.3 | 26.0 | 0.24 | 0.00 | B | 0.95 | no |
26028 | 15.3 | 3.5 | 0.30 | 1.00 | 1.00 | 0.98 | 1.00 | 0.14 | 350.2 | 4.4 | 0.00 | 0.00 | B | 1.30 | no |
26029 | 336.6 | 315.2 | 1.03 | 0.79 | 0.98 | 0.89 | 0.85 | 9.68 | 167.7 | 336.9 | 1.63 | 0.00 | M | 2.60 | si |
26030 | 662.4 | 204.0 | 1.10 | 0.95 | 0.98 | 0.95 | 0.97 | 239.16 | 741.0 | 482.8 | 5.19 | 0.00 | M | 0.28 | no |
26031 | 50.5 | 0.0 | 0.16 | 0.85 | 0.99 | 0.52 | 0.95 | 0.23 | 503.0 | 8.0 | 0.00 | 0.00 | B | 13.00 | no |
26032 | 34.6 | 0.0 | 0.23 | 0.99 | 1.00 | 0.95 | 1.00 | 0.11 | 329.4 | 7.9 | 0.00 | 0.00 | M | 1.60 | no |
26033 | 81.5 | 9.0 | 4.01 | 0.47 | 0.93 | 0.61 | 0.71 | 5.72 | 194.7 | 320.7 | 0.03 | 0.00 | A | 0.50 | no |
26034 | 17.8 | 2.1 | 0.42 | 0.99 | 1.00 | 0.96 | 0.99 | 0.18 | 532.0 | 7.2 | 0.00 | 0.00 | B | 0.93 | no |
26035 | 91.5 | 0.0 | 0.20 | 0.91 | 0.98 | 0.44 | 0.96 | 2.54 | 542.9 | 15.6 | 0.00 | 0.00 | M | 1.80 | no |
26036 | 52.3 | 69.3 | 0.38 | 0.95 | 1.00 | 0.91 | 0.99 | 7.28 | 639.3 | 12.4 | 0.43 | 0.00 | M | 0.07 | no |
26037 | 28.8 | 3.6 | 0.11 | 0.95 | 0.99 | 0.97 | 0.98 | 0.40 | 892.6 | 2.7 | 0.00 | 0.00 | B | 0.93 | no |
26038 | 78.7 | 12.9 | 0.06 | 0.99 | 1.00 | 0.93 | 0.99 | 0.35 | 190.3 | 4.4 | 0.00 | 0.00 | M | 2.40 | no |
26039 | 52.2 | 15.5 | 0.10 | 0.97 | 0.99 | 0.91 | 0.99 | 1.26 | 558.2 | 4.2 | 0.01 | 0.00 | B | 0.41 | no |
26040 | 119.4 | 1.7 | 0.02 | 0.71 | 0.99 | 0.60 | 0.90 | 0.25 | 337.9 | 2.0 | 0.00 | 0.00 | B | 24.00 | no |
26041 | 73.1 | 0.0 | 0.17 | 0.93 | 0.98 | 0.95 | 0.97 | 2.56 | 507.3 | 0.1 | 0.00 | 9.46 | B | 1.40 | no |
26042 | 117.1 | 277.0 | 4.62 | 0.75 | 0.97 | 0.81 | 0.78 | 31.50 | 527.3 | 502.6 | 6.62 | 0.00 | AA | 5.40 | no |
26043 | 73.9 | 626.7 | 0.39 | 0.96 | 0.90 | 0.89 | 0.99 | 23.36 | 273.6 | 3.8 | 1.71 | 0.00 | A | 0.45 | no |
26044 | 22.6 | 0.8 | 0.06 | 0.89 | 0.98 | 0.83 | 0.96 | 0.09 | 544.4 | 1.3 | 0.00 | 0.00 | M | 25.00 | no |
26045 | 94.3 | 0.8 | 0.16 | 0.72 | 0.96 | 0.67 | 0.91 | 0.50 | 520.4 | 14.5 | 0.18 | 0.00 | B | 0.72 | no |
26046 | 38.6 | 0.0 | 0.19 | 0.99 | 0.99 | 0.97 | 0.99 | 0.08 | 567.1 | 7.4 | 0.00 | 0.00 | B | 0.09 | no |
26047 | 413.9 | 0.0 | 0.09 | 0.83 | 0.98 | 0.75 | 0.95 | 0.37 | 105.1 | 28.4 | 0.42 | 7.01 | B | 0.04 | no |
26048 | 259.7 | 81.5 | 0.16 | 0.92 | 0.99 | 0.67 | 0.98 | 9.75 | 429.8 | 16.0 | 16.69 | 0.00 | M | 0.00 | no |
26049 | 156.4 | 1.6 | 0.06 | 0.49 | 0.85 | 0.67 | 0.75 | 0.47 | 448.7 | 8.2 | 0.00 | 0.00 | A | 29.00 | si |
26050 | 37.1 | 4.1 | 0.31 | 0.91 | 0.99 | 0.84 | 0.96 | 0.16 | 299.8 | 11.5 | 0.00 | 0.00 | B | 1.30 | no |
26051 | 151.4 | 0.0 | 0.03 | 0.59 | 0.98 | 0.70 | 0.90 | 0.48 | 262.8 | 4.5 | 0.20 | 0.00 | M | 40.00 | no |
26052 | 213.4 | 9.8 | 0.07 | 0.91 | 0.97 | 0.90 | 0.96 | 0.82 | 400.8 | 11.5 | 1.71 | 0.00 | M | 18.00 | no |
26053 | 6.4 | 1.0 | 0.08 | 1.00 | 1.00 | 0.99 | 1.00 | 0.04 | 296.2 | 0.5 | 0.00 | 0.00 | B | 2.70 | no |
26054 | 22.6 | 0.0 | 0.03 | 0.71 | 0.83 | 0.76 | 0.96 | 0.17 | 846.0 | 0.4 | 0.00 | 0.00 | B | 15.00 | no |
26056 | 47.2 | 7.0 | 1.30 | 0.36 | 0.97 | 0.83 | 0.89 | 0.23 | 69.1 | 61.0 | 0.01 | 0.00 | B | 0.20 | no |
26057 | 94.0 | 4.7 | 0.02 | 0.91 | 1.00 | 0.62 | 0.96 | 0.37 | 690.0 | 1.6 | 0.00 | 0.00 | M | 7.90 | no |
26058 | 62.4 | 0.0 | 0.61 | 0.95 | 0.99 | 0.81 | 0.96 | 5.00 | 842.8 | 31.8 | 1.53 | 0.00 | M | 0.08 | no |
26059 | 42.2 | 1.2 | 0.24 | 0.97 | 1.00 | 0.43 | 0.99 | 0.09 | 145.7 | 6.6 | 3.50 | 0.00 | B | 0.73 | no |
26060 | 56.0 | 5.5 | 0.21 | 0.91 | 0.98 | 0.77 | 0.96 | 0.21 | 365.4 | 10.9 | 0.50 | 0.00 | B | 0.03 | no |
26061 | 72.3 | 0.0 | 0.87 | 0.82 | 0.99 | 0.30 | 0.92 | 60.85 | 117395.3 | 1.7 | 0.35 | 0.00 | M | 18.00 | no |
26062 | 38.6 | 2.7 | 0.04 | 1.00 | 0.99 | 0.95 | 0.99 | 0.26 | 619.0 | 1.1 | 0.00 | 0.00 | M | 5.90 | no |
26063 | 32.9 | 3.2 | 0.01 | 0.86 | 1.00 | 0.95 | 0.98 | 0.12 | 256.2 | 0.2 | 0.00 | 0.00 | B | 3.90 | no |
26064 | 126.8 | 0.9 | 0.32 | 0.85 | 0.95 | 0.54 | 0.91 | 0.49 | 846.1 | 39.6 | 0.00 | 0.00 | B | 0.01 | no |
26065 | 73.8 | 1.1 | 0.19 | 0.94 | 0.95 | 0.32 | 0.92 | 0.22 | 498.3 | 14.1 | 0.00 | 0.00 | B | 0.07 | no |
26066 | 130.1 | 4.6 | 0.39 | 0.92 | 0.99 | 0.89 | 0.98 | 0.63 | 197.4 | 49.5 | 0.00 | 0.00 | M | 1.10 | no |
26067 | 62.0 | 3.1 | 0.57 | 0.99 | 1.00 | 0.90 | 0.95 | 0.14 | 259.0 | 35.1 | 0.00 | 0.00 | B | 0.99 | no |
26068 | 47.4 | 0.0 | 0.07 | 0.91 | 0.98 | 0.86 | 0.97 | 0.24 | 563.7 | 2.5 | 0.40 | 0.00 | B | 3.40 | no |
26069 | 112.3 | 4.3 | 0.01 | 0.52 | 0.95 | 0.54 | 0.66 | 1.56 | 710.0 | 0.0 | 0.00 | 0.00 | A | 27.00 | no |
26070 | 154.1 | 20.5 | 0.45 | 0.86 | 0.98 | 0.78 | 0.96 | 3.04 | 492.4 | 64.1 | 1.81 | 0.00 | B | 0.03 | no |
26071 | 15.6 | 0.0 | 15.37 | 0.62 | 0.99 | 0.77 | 0.89 | 2.69 | 335.4 | 236.3 | 0.00 | 0.00 | A | 0.07 | no |
26072 | 58.3 | 0.0 | 4.58 | 0.46 | 0.94 | 0.69 | 0.65 | 2.43 | 458.2 | 264.4 | 0.02 | 0.00 | A | 0.09 | no |
Mínimo | 15.1 | 0.0 | 0.01 | 106.3 | 0.00 | ||||||||||
Máximo | 416.8 | 628.0 | 8.32 | 1092.2 | 38.15 |
Fuente: elaboración propia.
Anexo 7 – Variables normalizadas de las 5 dimensiones del IPh.
Clave INEGI | R1 | R2 | R3 | A1 | A2 | C1 | C2 | C3 | U1 | U2 | U3 | U4 | E1 | E2 | E3 |
8031 | 0.56 | 0.06 | 0.92 | 0.69 | 0.53 | 0.73 | 0.84 | 0.55 | 0.46 | 0.78 | 0.83 | 0.00 | 0.67 | 0.18 | 1.00 |
8040 | 0.88 | 0.08 | 1.00 | 0.73 | 0.59 | 0.74 | 0.85 | 0.55 | 0.66 | 0.63 | 0.85 | 0.00 | 0.33 | 0.71 | 1.00 |
8043 | 0.04 | 0.01 | 0.99 | 0.76 | 0.60 | 0.73 | 0.83 | 0.56 | 0.88 | 0.77 | 0.83 | 0.00 | 1.00 | 0.12 | 1.00 |
8047 | 0.15 | 0.00 | 1.00 | 0.35 | 0.20 | 0.63 | 0.75 | 0.48 | 0.09 | 0.00 | 0.69 | 0.00 | 1.00 | 1.00 | 1.00 |
8051 | 0.15 | 0.00 | 1.00 | 0.48 | 0.26 | 0.73 | 0.78 | 0.49 | 0.15 | 0.00 | 0.66 | 0.00 | 1.00 | 1.00 | 1.00 |
8063 | 0.41 | 0.01 | 1.00 | 0.69 | 0.53 | 0.00 | 0.75 | 0.00 | 0.68 | 0.58 | 0.75 | 0.00 | 1.00 | 0.37 | 0.00 |
8066 | 0.24 | 0.00 | 1.00 | 0.20 | 0.17 | 0.59 | 0.68 | 0.46 | 0.00 | 0.00 | 0.68 | 0.00 | 1.00 | 0.89 | 0.00 |
26001 | 0.00 | 0.01 | 0.95 | 0.98 | 0.78 | 0.79 | 0.88 | 0.59 | 0.81 | 0.83 | 0.87 | 0.00 | 1.00 | 0.04 | 1.00 |
26002 | 0.38 | 0.32 | 0.98 | 0.94 | 0.86 | 0.80 | 0.92 | 0.64 | 1.00 | 0.55 | 0.64 | 0.00 | 0.67 | 0.05 | 1.00 |
26003 | 0.64 | 0.03 | 0.73 | 0.38 | 0.35 | 0.75 | 0.79 | 0.58 | 0.75 | 0.77 | 0.78 | 0.00 | 0.00 | 0.89 | 0.00 |
26004 | 0.43 | 0.01 | 0.96 | 0.84 | 0.75 | 0.78 | 0.89 | 0.59 | 0.82 | 0.85 | 0.87 | 0.00 | 0.67 | 0.00 | 1.00 |
26005 | 0.03 | 0.00 | 0.99 | 0.97 | 0.88 | 0.80 | 0.80 | 0.58 | 0.51 | 0.67 | 0.80 | 0.00 | 1.00 | 0.47 | 1.00 |
26006 | 0.28 | 0.01 | 0.99 | 0.95 | 0.76 | 0.78 | 0.85 | 0.57 | 0.51 | 0.81 | 0.85 | 0.00 | 0.67 | 0.03 | 1.00 |
26007 | 0.00 | 0.00 | 0.98 | 0.95 | 0.98 | 0.89 | 0.88 | 0.59 | 0.60 | 0.84 | 0.88 | 0.00 | 1.00 | 0.00 | 1.00 |
26008 | 0.07 | 0.01 | 1.00 | 0.92 | 0.58 | 0.76 | 0.84 | 0.52 | 0.89 | 0.42 | 0.84 | 0.00 | 1.00 | 0.19 | 1.00 |
26009 | 0.08 | 0.00 | 1.00 | 0.92 | 0.79 | 0.83 | 0.81 | 0.54 | 0.55 | 0.76 | 0.81 | 0.00 | 0.67 | 0.50 | 1.00 |
26010 | 0.10 | 0.00 | 0.99 | 0.81 | 0.34 | 0.73 | 0.79 | 0.54 | 0.73 | 0.75 | 0.79 | 0.00 | 1.00 | 0.34 | 1.00 |
26011 | 0.09 | 0.00 | 1.00 | 0.96 | 0.54 | 0.74 | 0.89 | 0.60 | 0.37 | 0.73 | 0.89 | 0.00 | 0.67 | 0.01 | 1.00 |
26012 | 0.13 | 0.00 | 0.68 | 0.72 | 0.71 | 0.74 | 0.85 | 0.60 | 0.87 | 0.84 | 0.85 | 0.00 | 0.33 | 0.04 | 0.00 |
26013 | 0.05 | 0.01 | 0.97 | 0.99 | 0.93 | 0.78 | 0.86 | 0.62 | 0.48 | 0.81 | 0.84 | 0.00 | 1.00 | 0.04 | 1.00 |
26014 | 0.05 | 0.01 | 0.96 | 0.98 | 0.59 | 0.81 | 0.87 | 0.61 | 0.61 | 0.82 | 0.87 | 0.00 | 1.00 | 0.03 | 1.00 |
26015 | 0.14 | 0.01 | 0.98 | 0.94 | 0.26 | 0.73 | 0.87 | 0.53 | 0.75 | 0.86 | 0.87 | 0.00 | 1.00 | 0.13 | 1.00 |
26016 | 0.11 | 0.02 | 0.97 | 0.95 | 0.92 | 0.80 | 0.88 | 0.63 | 0.00 | 0.75 | 0.88 | 0.00 | 0.67 | 0.00 | 1.00 |
26017 | 1.00 | 1.00 | 0.98 | 0.79 | 0.72 | 0.80 | 0.88 | 0.63 | 0.84 | 0.66 | 0.76 | 0.00 | 0.67 | 0.00 | 0.00 |
26018 | 0.47 | 1.00 | 0.05 | 0.94 | 0.94 | 0.80 | 0.92 | 0.72 | 0.46 | 0.86 | 0.91 | 0.00 | 0.67 | 0.14 | 1.00 |
26019 | 0.20 | 0.04 | 0.92 | 0.98 | 0.93 | 0.82 | 0.94 | 0.70 | 0.53 | 0.43 | 0.54 | 0.00 | 0.67 | 0.03 | 1.00 |
26020 | 0.23 | 0.02 | 0.97 | 0.92 | 0.88 | 0.79 | 0.86 | 0.58 | 0.93 | 0.85 | 0.86 | 0.00 | 0.67 | 0.00 | 1.00 |
26021 | 0.39 | 0.00 | 0.99 | 0.70 | 0.61 | 0.78 | 0.82 | 0.55 | 0.34 | 0.75 | 0.78 | 0.00 | 0.67 | 0.05 | 1.00 |
26022 | 0.13 | 0.00 | 0.99 | 0.90 | 0.62 | 0.80 | 0.82 | 0.55 | 0.70 | 0.80 | 0.82 | 0.00 | 1.00 | 0.02 | 1.00 |
26023 | 0.17 | 0.01 | 0.98 | 0.95 | 0.64 | 0.79 | 0.89 | 0.67 | 0.70 | 0.78 | 0.83 | 0.00 | 1.00 | 0.04 | 1.00 |
26024 | 0.00 | 0.00 | 1.00 | 0.95 | 0.97 | 0.80 | 0.86 | 0.62 | 0.82 | 0.67 | 0.86 | 0.00 | 1.00 | 0.05 | 1.00 |
26025 | 0.02 | 0.13 | 0.74 | 0.72 | 0.75 | 0.80 | 0.90 | 0.66 | 0.85 | 0.82 | 0.90 | 0.00 | 0.67 | 0.00 | 1.00 |
26026 | 0.06 | 0.00 | 0.00 | 0.49 | 0.37 | 0.73 | 0.82 | 0.63 | 0.92 | 0.82 | 0.82 | 0.00 | 0.00 | 0.00 | 0.00 |
26027 | 0.24 | 0.00 | 0.97 | 0.94 | 0.89 | 0.80 | 0.92 | 0.64 | 0.93 | 0.89 | 0.91 | 0.00 | 1.00 | 0.02 | 1.00 |
26028 | 0.00 | 0.01 | 0.97 | 0.99 | 0.98 | 0.84 | 0.89 | 0.63 | 0.75 | 0.86 | 0.89 | 0.00 | 1.00 | 0.03 | 1.00 |
26029 | 0.80 | 0.50 | 0.88 | 0.77 | 0.76 | 0.81 | 0.90 | 0.68 | 0.94 | 0.87 | 0.89 | 0.00 | 0.67 | 0.07 | 0.00 |
26030 | 1.00 | 0.32 | 0.87 | 0.93 | 0.92 | 0.86 | 0.90 | 0.76 | 0.36 | 0.60 | 0.90 | 0.00 | 0.67 | 0.01 | 1.00 |
26031 | 0.09 | 0.00 | 0.98 | 0.84 | 0.49 | 0.76 | 0.85 | 0.56 | 0.60 | 0.83 | 0.85 | 0.00 | 1.00 | 0.34 | 1.00 |
26032 | 0.05 | 0.00 | 0.97 | 0.99 | 0.95 | 0.82 | 0.87 | 0.63 | 0.77 | 0.85 | 0.87 | 0.00 | 0.67 | 0.04 | 1.00 |
26033 | 0.17 | 0.01 | 0.52 | 0.44 | 0.43 | 0.76 | 0.87 | 0.66 | 0.91 | 0.85 | 0.87 | 0.00 | 0.33 | 0.01 | 1.00 |
26034 | 0.01 | 0.00 | 0.95 | 0.99 | 0.95 | 0.90 | 0.87 | 0.65 | 0.57 | 0.85 | 0.87 | 0.00 | 1.00 | 0.02 | 1.00 |
26035 | 0.19 | 0.00 | 0.98 | 0.90 | 0.42 | 0.81 | 0.89 | 0.61 | 0.56 | 0.77 | 0.89 | 0.00 | 0.67 | 0.05 | 1.00 |
26036 | 0.09 | 0.11 | 0.96 | 0.95 | 0.90 | 0.81 | 0.92 | 0.67 | 0.46 | 0.56 | 0.90 | 0.00 | 0.67 | 0.00 | 1.00 |
26037 | 0.03 | 0.01 | 0.99 | 0.94 | 0.95 | 0.79 | 0.86 | 0.62 | 0.20 | 0.74 | 0.86 | 0.00 | 1.00 | 0.02 | 1.00 |
26038 | 0.16 | 0.02 | 0.99 | 0.99 | 0.92 | 0.84 | 0.89 | 0.74 | 0.91 | 0.82 | 0.89 | 0.00 | 0.67 | 0.06 | 1.00 |
26039 | 0.09 | 0.02 | 0.99 | 0.96 | 0.90 | 0.82 | 0.90 | 0.62 | 0.54 | 0.69 | 0.90 | 0.00 | 1.00 | 0.01 | 1.00 |
26040 | 0.26 | 0.00 | 1.00 | 0.71 | 0.54 | 0.68 | 0.81 | 0.51 | 0.77 | 0.72 | 0.81 | 0.00 | 1.00 | 0.63 | 1.00 |
26041 | 0.14 | 0.00 | 0.98 | 0.92 | 0.92 | 0.86 | 0.90 | 0.67 | 0.59 | 0.01 | 0.90 | 0.78 | 1.00 | 0.04 | 1.00 |
26042 | 0.25 | 0.44 | 0.45 | 0.73 | 0.63 | 0.78 | 0.88 | 0.70 | 0.57 | 0.82 | 0.87 | 0.00 | 0.00 | 0.14 | 1.00 |
26043 | 0.15 | 1.00 | 0.95 | 0.87 | 0.88 | 0.83 | 0.93 | 0.71 | 0.83 | 0.12 | 0.88 | 0.00 | 0.33 | 0.01 | 1.00 |
26044 | 0.02 | 0.00 | 0.99 | 0.87 | 0.79 | 0.84 | 0.83 | 0.55 | 0.56 | 0.77 | 0.83 | 0.00 | 0.67 | 0.66 | 1.00 |
26045 | 0.20 | 0.00 | 0.98 | 0.70 | 0.61 | 0.77 | 0.82 | 0.54 | 0.58 | 0.78 | 0.81 | 0.00 | 1.00 | 0.02 | 1.00 |
26046 | 0.06 | 0.00 | 0.98 | 0.98 | 0.97 | 0.90 | 0.86 | 0.56 | 0.53 | 0.85 | 0.86 | 0.00 | 1.00 | 0.00 | 1.00 |
26047 | 0.99 | 0.00 | 0.99 | 0.82 | 0.72 | 0.82 | 0.87 | 0.63 | 1.00 | 0.68 | 0.86 | 0.19 | 1.00 | 0.00 | 1.00 |
26048 | 0.61 | 0.13 | 0.98 | 0.91 | 0.66 | 0.79 | 0.92 | 0.66 | 0.67 | 0.34 | 0.56 | 0.00 | 0.67 | 0.00 | 1.00 |
26049 | 0.35 | 0.00 | 0.99 | 0.42 | 0.50 | 0.68 | 0.73 | 0.51 | 0.65 | 0.69 | 0.73 | 0.00 | 0.33 | 0.76 | 0.00 |
26050 | 0.05 | 0.01 | 0.96 | 0.90 | 0.81 | 0.76 | 0.81 | 0.56 | 0.80 | 0.80 | 0.81 | 0.00 | 1.00 | 0.03 | 1.00 |
26051 | 0.34 | 0.00 | 1.00 | 0.58 | 0.63 | 0.74 | 0.77 | 0.55 | 0.84 | 0.67 | 0.74 | 0.00 | 0.67 | 1.00 | 1.00 |
26052 | 0.49 | 0.02 | 0.99 | 0.88 | 0.86 | 0.78 | 0.84 | 0.59 | 0.70 | 0.69 | 0.73 | 0.00 | 0.67 | 0.47 | 1.00 |
26053 | 0.00 | 0.00 | 0.99 | 1.00 | 0.98 | 0.86 | 0.88 | 0.61 | 0.81 | 0.81 | 0.88 | 0.00 | 1.00 | 0.07 | 1.00 |
26054 | 0.02 | 0.00 | 1.00 | 0.60 | 0.73 | 0.88 | 0.84 | 0.58 | 0.25 | 0.60 | 0.84 | 0.00 | 1.00 | 0.39 | 1.00 |
26056 | 0.08 | 0.01 | 0.85 | 0.35 | 0.74 | 0.77 | 0.78 | 0.45 | 1.00 | 0.78 | 0.78 | 0.00 | 1.00 | 0.01 | 1.00 |
26057 | 0.20 | 0.01 | 1.00 | 0.90 | 0.59 | 0.81 | 0.81 | 0.57 | 0.41 | 0.66 | 0.81 | 0.00 | 0.67 | 0.21 | 1.00 |
26058 | 0.12 | 0.00 | 0.93 | 0.94 | 0.78 | 0.81 | 0.91 | 0.66 | 0.25 | 0.75 | 0.87 | 0.00 | 0.67 | 0.00 | 1.00 |
26059 | 0.07 | 0.00 | 0.97 | 0.97 | 0.42 | 0.74 | 0.88 | 0.57 | 0.96 | 0.57 | 0.58 | 0.00 | 1.00 | 0.02 | 1.00 |
26060 | 0.10 | 0.01 | 0.98 | 0.89 | 0.74 | 0.77 | 0.86 | 0.54 | 0.74 | 0.80 | 0.82 | 0.00 | 1.00 | 0.00 | 1.00 |
26061 | 0.14 | 0.00 | 0.90 | 0.81 | 0.27 | 0.79 | 0.82 | 0.50 | 0.00 | 0.02 | 0.81 | 0.00 | 0.67 | 0.47 | 1.00 |
26062 | 0.06 | 0.00 | 1.00 | 0.98 | 0.94 | 0.82 | 0.85 | 0.55 | 0.48 | 0.69 | 0.85 | 0.00 | 0.67 | 0.15 | 1.00 |
26063 | 0.04 | 0.01 | 1.00 | 0.86 | 0.93 | 0.82 | 0.85 | 0.62 | 0.85 | 0.51 | 0.85 | 0.00 | 1.00 | 0.10 | 1.00 |
26064 | 0.28 | 0.00 | 0.96 | 0.81 | 0.49 | 0.78 | 0.82 | 0.55 | 0.25 | 0.81 | 0.82 | 0.00 | 1.00 | 0.00 | 1.00 |
26065 | 0.15 | 0.00 | 0.98 | 0.90 | 0.29 | 0.78 | 0.82 | 0.53 | 0.60 | 0.81 | 0.82 | 0.00 | 1.00 | 0.00 | 1.00 |
26066 | 0.29 | 0.01 | 0.96 | 0.91 | 0.87 | 0.83 | 0.86 | 0.63 | 0.91 | 0.85 | 0.86 | 0.00 | 0.67 | 0.03 | 1.00 |
26067 | 0.12 | 0.00 | 0.93 | 0.98 | 0.85 | 0.78 | 0.86 | 0.61 | 0.85 | 0.86 | 0.86 | 0.00 | 1.00 | 0.03 | 1.00 |
26068 | 0.08 | 0.00 | 0.99 | 0.89 | 0.84 | 0.73 | 0.85 | 0.57 | 0.54 | 0.68 | 0.74 | 0.00 | 1.00 | 0.09 | 1.00 |
26069 | 0.24 | 0.01 | 1.00 | 0.49 | 0.35 | 0.70 | 0.77 | 0.52 | 0.39 | 0.02 | 0.77 | 0.00 | 0.33 | 0.71 | 1.00 |
26070 | 0.35 | 0.03 | 0.95 | 0.84 | 0.75 | 0.00 | 0.87 | 0.00 | 0.61 | 0.81 | 0.85 | 0.00 | 1.00 | 0.00 | 1.00 |
26071 | 0.00 | 0.00 | 0.00 | 0.61 | 0.69 | 0.76 | 0.86 | 0.64 | 0.77 | 0.85 | 0.86 | 0.00 | 0.33 | 0.00 | 1.00 |
26072 | 0.11 | 0.00 | 0.45 | 0.43 | 0.45 | 0.74 | 0.84 | 0.60 | 0.64 | 0.84 | 0.84 | 0.00 | 0.33 | 0.00 | 1.00 |
Fuente: elaboración propia.
Revista IDeAS, Rio de Janeiro, volume 15, 1-33, e021005, jan./dez. 2021 • ISSN 1984-9834
[1]Doctorante en Desarrollo Regional en el Centro de Investigación en Alimentación y Desarrollo A.C., Hermosillo, Sonora, México. E-mail: juliana.olivas@estudiantes.ciad.mx
[2]Investigador titular “E” en Centro de Investigación en Alimentación y Desarrollo A.C., Departamento de Economía, Hermosillo, Sonora, México. E-mail: mcamberos@ciad.mx
[3]Este trabajo comprende parte de los resultados obtenidos en la tesis de doctorado del primer autor, con asesoría del coautor. Se agradece al Consejo Nacional de Ciencia y Tecnología (Conacyt), institución que financió los estudios de doctorado en Desarrollo Regional en el Centro de Alimentación y Desarrollo A.C. (CIAD).
[4]Agua segura: Disponible en la vivienda todo el tiempo, asequible, y libre de contaminación (ONU, 2015).
[5]Saneamiento seguro: Viviendas conectadas a una red de drenaje o tratamiento de las excretas en el sitio (ibid).
[6] Real Statistics Resource Pack: Disponible en https://www.real-statistics.com. Acceso en: 18 mayo 2020.